Mathematics for Elementary Teachers
Sequences
Sequence: an ordered list of objects, events, or numbers
Types of Sequences
Recurrence relationship Sequences
Defines a sequence in which the current term is dependent on previous term(s)
Difference: multiply by 2 then add 1
13 multiplied by 2 equals 26 then add 1
Product of 1st term 13
ex. 6, 13, 27, 55..
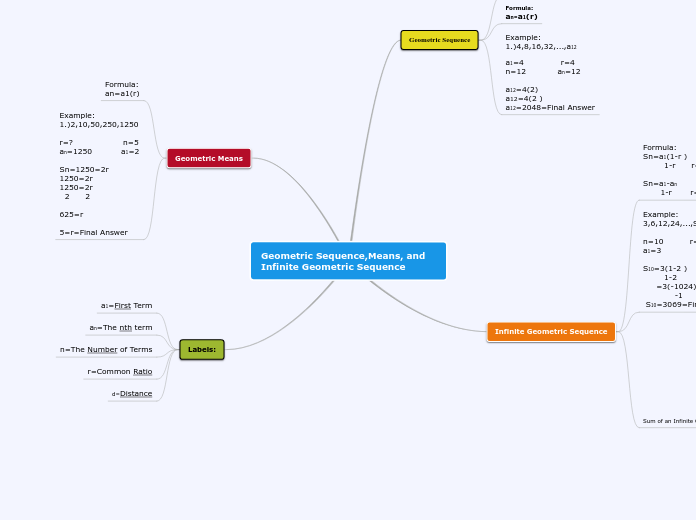
Geometric Sequences
Sequence of numbers with a common ratio
common ratio -1/2
ex. 8, -4, 2,-1,..
Arithmetic Sequences
Sequences or numbers with a common difference
Adding 2 to each time will create the next number
common difference of 2, 4, 6, 8 is 2
ex. 2, 4, 6, 8, 10
Composed of elements (objects found within)
Problem Solving
Steps
4. Look back (reflect)
Is there an easier way to solve it?
Does it need to be revised?
Does the answer make sense?
Subtopic
3. Carry out the plan
Revise the plan if necessary
If the solution is not visible, rethink the plan
Be persistant with your current plan
2. Devise a plan
Use a model
Create charts, lists, and use objects
Work backwards
Solve a simpler problem
Use an easier problem based on your current problem
Guess and check
Think of solutions and plug into the problem to check answer
1. Identify the problem
Understand the problem
George Polya (1887-1985)
Major contribution was his work in Problem Solving
"..'solving a problem means finding a way out of difficulty, a way around an obstacle, attaining an aim which was not immediately attainable'.." (Billstein 2)
Quote by George Polya pulled from Mathematical Discovery and re quoted in A Problem Solving Approach to Mathematics for Elementary School Teachers 11th edition by Rick Billstein.
Mathematician and Teacher of 20th Century