Medidas de Tendencia central y Dispersión
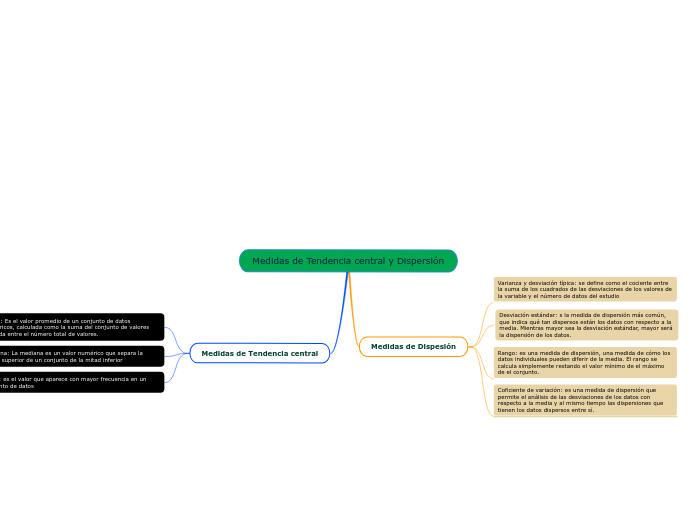
Medidas de Tendencia central
Moda: es el valor que aparece con mayor frecuencia en un conjunto de datos
Difícil de interpretar si los datos tiene 3 o más modas.
En ocasiones, el azar hace que una sola observación no represente el valor más frecuente del conjunto de datos.
No siempre existe, si los datos no se repiten.
No utiliza toda la información disponible.
Para conjuntos pequeños de datos su valor no tiene casi utilidad, si es que de hecho existe. Solo tiene significado en el caso de una gran cantidad de datos.
Se puede calcular en clases de extremo abierto.
Fácil de interpretar.
Puede usarse para datos tanto cuantitativos como cualitativos.
No requiere cálculos.
Mediana: La mediana es un valor numérico que separa la mitad superior de un conjunto de la mitad inferior
Hay que ordenar los datos antes de determinarla.
No pondera cada valor por el número de veces que se ha repetido.
No utiliza en su “cálculo” toda la información disponible.
Es la medida de tendencia central más representativa en el caso de variables que solo admiten la escala ordinal.
Se puede calcular para cualquier tipos de datos cuantitativos, incluso los datos con clase de extremo abierto.
Fácil de entender.
No se ve influenciada por valores extremos, ya que solo influyen los valores centrales.
Fácil de calcular si el número de observaciones no es muy grande.
Media: Es el valor promedio de un conjunto de datos numéricos, calculada como la suma del conjunto de valores dividida entre el número total de valores.
Desventajas
No se puede calcular para datos que tengan clases de extremo abierto, tanto superior como inferior.
Si el conjunto de datos es muy grande puede ser tedioso su cálculo manual.
No se puede calcular para datos cualitativos.
No es recomendable emplearla en distribuciones muy asimétricas.
Es sensible a los valores extremos.
Ventajas
Presenta rigor matemático.
Se emplea a menudo en cálculos estadísticos posteriores.
Es sensible a cualquier cambio en los datos
El promedio es estable en el muestreo
Es la medida de tendencia central más usada
Medidas de Dispesión
Coficiente de variación: es una medida de dispersión que permite el análisis de las desviaciones de los datos con respecto a la media y al mismo tiempo las dispersiones que tienen los datos dispersos entre sí.
Rango: es una medida de dispersión, una medida de cómo los datos individuales pueden diferir de la media. El rango se calcula simplemente restando el valor mínimo de el máximo de el conjunto.
Desviación estándar: s la medida de dispersión más común, que indica qué tan dispersos están los datos con respecto a la media. Mientras mayor sea la desviación estándar, mayor será la dispersión de los datos.
Varianza y desviación típica: se define como el cociente entre la suma de los cuadrados de las desviaciones de los valores de la variable y el número de datos del estudio