door ANGEL LOPEZ 4 jaren geleden
482
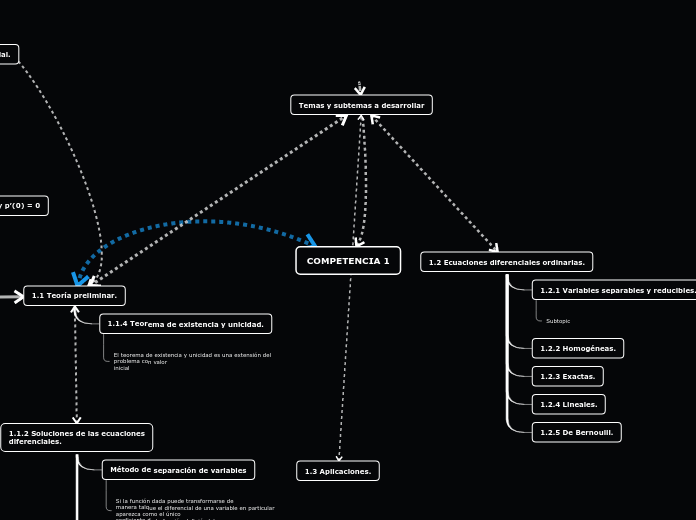
Organigrama arbol
Las ecuaciones diferenciales se dividen en varias categorías, cada una con sus propias características y métodos de solución. Las ecuaciones diferenciales ordinarias se destacan por su importancia y se clasifican en homogéneas, exactas, lineales y no lineales, entre otras.