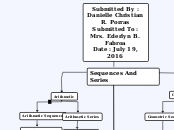
Sequences And Series
Submitted By : Danielle Christian R. Porras
Submitted To : Mrs. Ederlyn B. Fabroa
Date : July 19, 2016
Fibonacci Sequence
A fibonacci sequence is
a sequence where the
previous term is added
to the next term.
Example :
0, 1, 1, 2, 3,
5, 8, 13, 21, 34,
55, 89, 144, 233, 377
Harmonic Sequence
A harmonic sequence is
a sequence where the
reciprocals of the terms
form an arithmetic sequence.
Examples :
1, 1/2, 1/3, 1/4, 1/5
1, 1/16, 1/33, 1/50, 1/67, 1/84
1, -1/3, -1/7, -1/11, -1/15
Geometric
Geometric Series
A geometric series is
the sum of all the terms
of a geometric sequence.
Examples :
1, 2, 4, 8, 16 S5 = 31
1, 3, 9, 27, 81 S5 = 121
1, 5, 25, 125, 625 S5 = 781
Formula : (Finite)
Sn = A1 (1-r^n)
(-------)
( 1-r )
or
Sn = A1 (r^n-1)
(-------)
( r-1 )
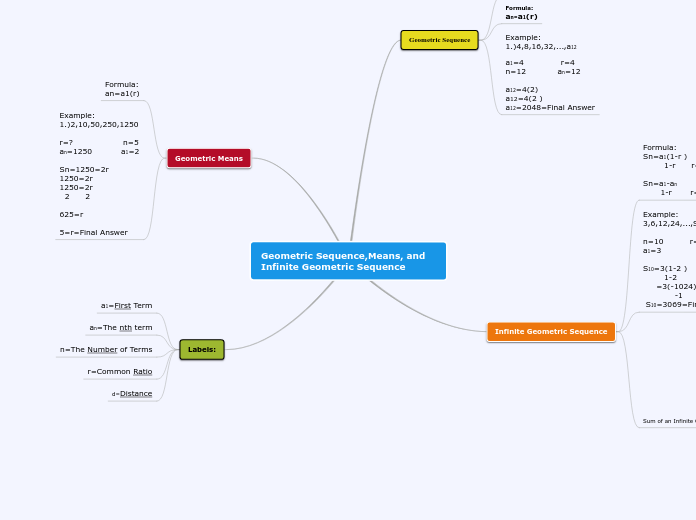
Formula : (Infinite)
Sn = A1/r-1
Geometric Sequence
A geometric sequence is
a sequence where a common
ratio is multiplied to each
consecutive term.
Examples :
1, 2, 4, 8, 16 r = 2
1, 3, 9, 27, 81 r = 3
1, 5, 25, 125, 625 r = 5
Formula :
An = A1r^n-1
Arithmetic
Arithmetic Series
An arithmetic series
is the sum of all the
terms of an arithmetic
sequence.
Examples :
1, 2, 3, 4, 5 S5 = 15
16, 33, 50, 67, 84 S5 = 250
1, -3, -7, -11, -15 S5 = -35
Formula :
Sn = n/2 (A1+An)
Arithmetic Sequence
An arithmetic sequence
is a sequence where a
common difference is
added to each consecutive
term.
Examples :
1, 2, 3, 4, 5 d = 1
16, 33, 50, 67, 84 d = 17
1, -3, -7, -11, -15 d = -4
Formula :
An = A1 + (n-1) d