door Charity Combs 10 maanden geleden
171
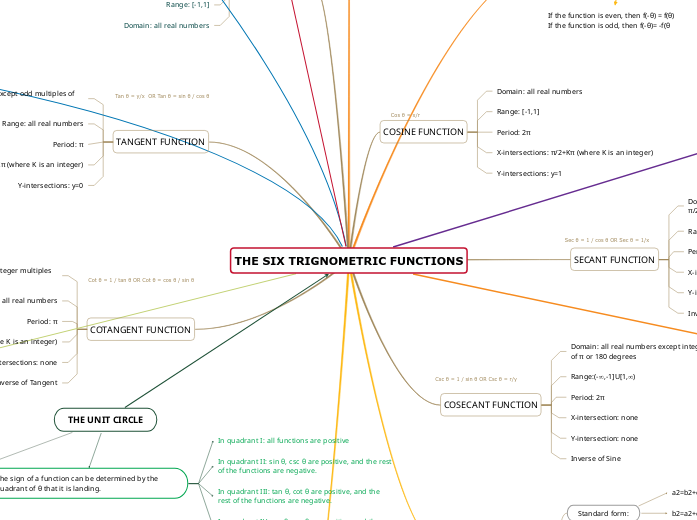
THE SIX TRIGNOMETRIC FUNCTIONS
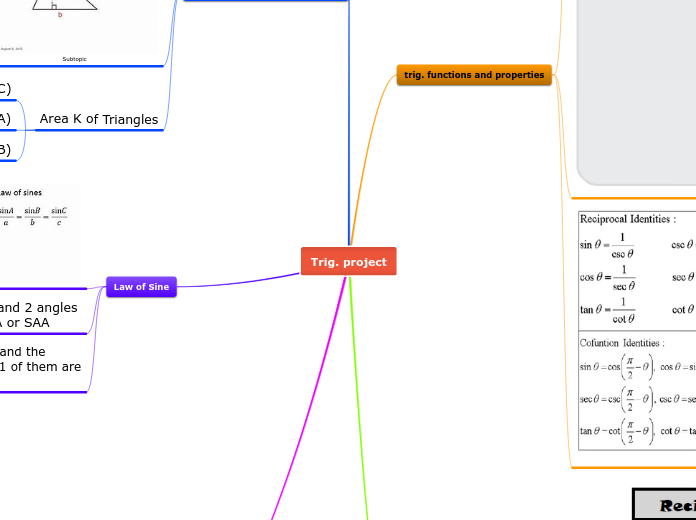
The unit circle is a fundamental concept in trigonometry that helps to understand the periodicity and behavior of trigonometric functions. It shows how functions like sine, cosine, tangent, and their reciprocals (