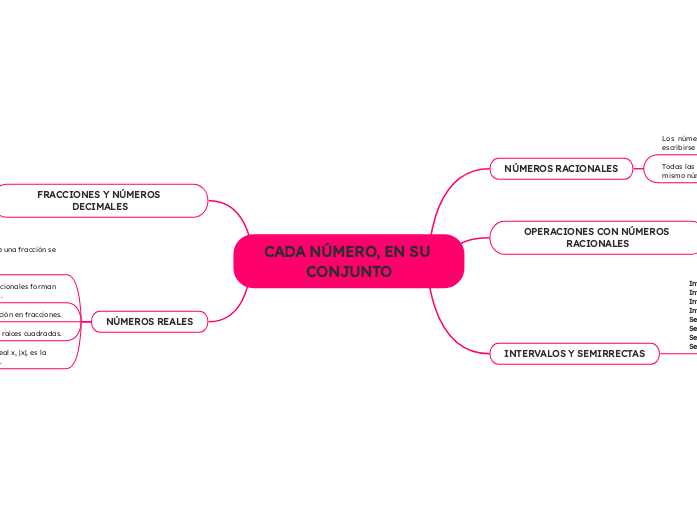
CADA NÚMERO, EN SU CONJUNTO
NÚMEROS REALES
El valor absoluto de un número real x, |x|, es la distancia entre el número x y el 0.
Representación de raíces cuadradas.
Representación en fracciones.
Los números racionales y los irracionales forman el conjunto de los números reales.
2,29148
Los números que no provienen de una fracción se denominan irracionales.
EJEMPLO: 1,89274024
FRACCIONES Y NÚMEROS DECIMALES
EJEMPLO: 1,2342 1-|12|342/9900=-12341/9900
Para escribir en forma de fracción un número decimal periódico se sigue esta regla:
Numero sin la coma y sin el arco del periódo x=____-____ Parte no periódica del numero sin la coma Tantos nueves como cifras tenga el periódo Tantos ceros como cifras tenga el anteperiódo
Una fracción se puede escribir en forma de decimal dividiendo el numerador entre el
denominador.
INTERVALOS Y SEMIRRECTAS
Intervalo abierto= (−2, 1), −2 < x < 1
Intervalo cerrado= [−2, 1], −2 ≤ x ≤ 1
Intervalo abierto por la izquierda= (−2, 1], −2 < x ≤ 1
Intervalo abierto por la derecha= [−2, 1), −2 ≤ x < 1
Semirrecta abierta por la izquierda= (1, +∞), x > 1
Semirrecta cerrada por la izquierda= [1, +∞), x ≥ 1
Semirrecta abierta por la derecha= (−∞, 1), x ≥ 1
Semirrecta cerrada por la derecha= (−∞, 1], x ≤ 1
OPERACIONES CON NÚMEROS RACIONALES
COCIENTE: A/B:C/D= A/B·D/C= A·D/B·C
EJEMPLO: 3/6:4/6= 3x4/6x4
PRODUCTO: A/B·C/D= A·C/B·D
EJEMPLO: 3/6x4/6= 3x4/6x6
RESTA: A/M-B/M= A-B/M
EJEMPLO: 3/6-4/6= 3-4/6
SUMA: A/M+B/M= A+B/M
EJEMPLO: 3/6+4/6= 3+4/6
NÚMEROS RACIONALES
Todas las fracciones equivalentes representan el mismo número racional
EJEMPLO: 8/4=1/2
Los números racionales son los que pueden escribirse en forma de fracción
EJEMPLO: 1/4