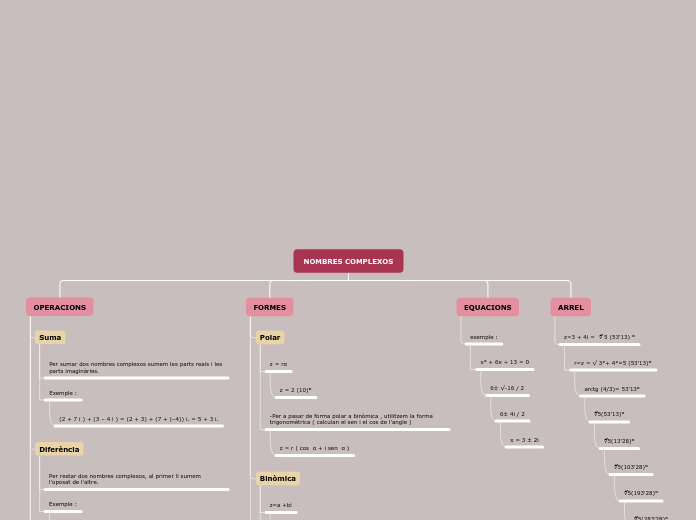
NOMBRES COMPLEXOS

Mer som dette

Familia Rodrigue Rodriguez

Ved Yised Natalia Rodiguez Rodriguez

familia cruz

Ved norelia ceballos cruz

SINTAGMAS

Ved Dereek Salcedo

USO CORRECTO DE LAS MAYUSCULAS

Ved Gabriela Pascacio

NOMBRES COMPLEXOS

ARREL

z=3 + 4i = ∜ 5 (53'13) º

r=z = √ 3²+ 4²=5 (53'13)º

arctg (4/3)= 53'13º

∜5(53'13)º

∜5(13'28)º

∜5(103'28)º

∜5(193'28)º

∜5(283'28)º

EQUACIONS

exemple :

x² + 6x + 13 = 0

6± √-16 / 2

6± 4i / 2

x = 3 ± 2i

FORMES

Trigonomètrica

z = 2 ( cos 140 + i sen 260 )

Binòmica

Per a pasar de binòmica a polar es calcula el mòdul ( z=√ a²+b² i la arctg ( b/a )

z=a +bi

z = 7 + 3i

Polar

-Per a pasar de forma polar a binòmica , utilitzem la forma trigonomètrica ( calculan el sen i el cos de l'angle )

z = r ( cos α + i sen α )

z = rα

z = 2 (10)º

OPERACIONS

Divisió

(2+3i / 1- i ) = (2+3i) · (1+i) / (1-i)·(1+i) = ( 2 + 2i +3i -3)/ (1+1) = -1+5i /2

Per a dividir els nobres complexos hi ha que racionalitzar per a eliminar la i del denominador.

Multiplicació

(2 + 3 i) · ( 4 + 5 i ) = ( 8 + 10 i + 12 i -15 ) = -7 + 22 i

Per a realitzar una multiplicació amb nombres complexos es realitza com una normal.

Diferència

(3-2 i) - ( 4+6 i ) = 1-8 i

Per restar dos nombres complexos, al primer li sumem l'oposat de l'altre.

Suma

Exemple :

(2 + 7 i ) + (3 – 4 i ) = (2 + 3) + (7 + (–4)) i. = 5 + 3 i.

Per sumar dos nombres complexos sumem les parts reals i les parts imaginàries.