av Carlos Angel 2 år siden
296
Tema 1: Números naturales

av Carlos Angel 2 år siden
296

Mer som dette
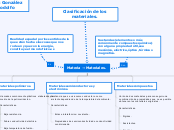

Ved Karla R.
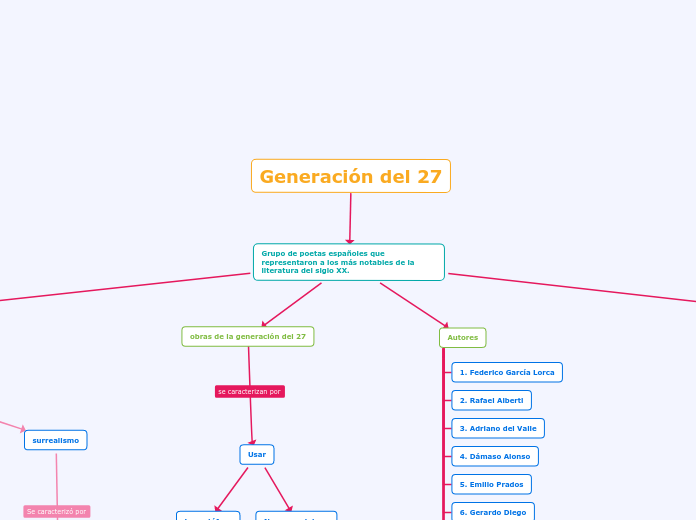

Ved william rodriguez
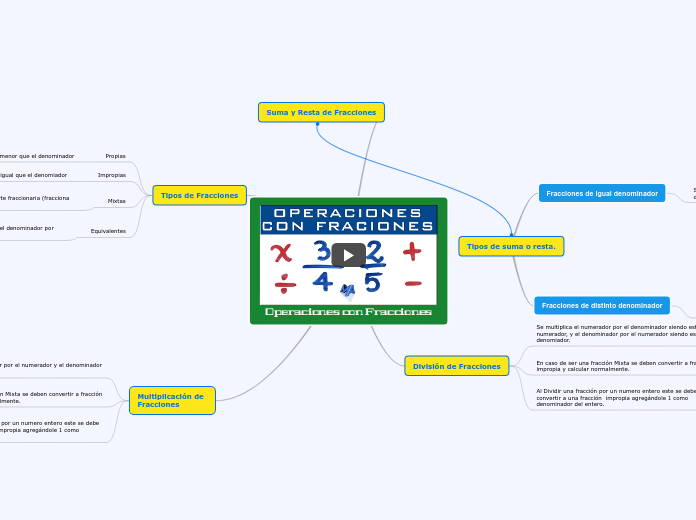

Ved Hermes Sanchez
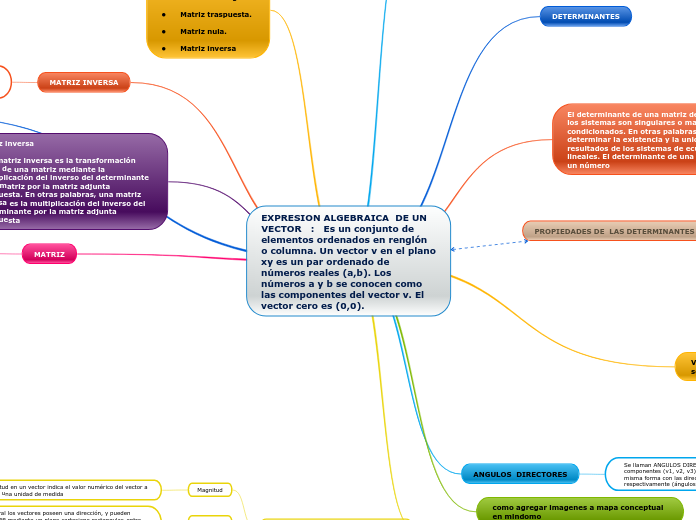

Ved Deisy Yolanda Amortegui Sanchez