av Hassan Zeeshan 3 år siden
303
VECTORS
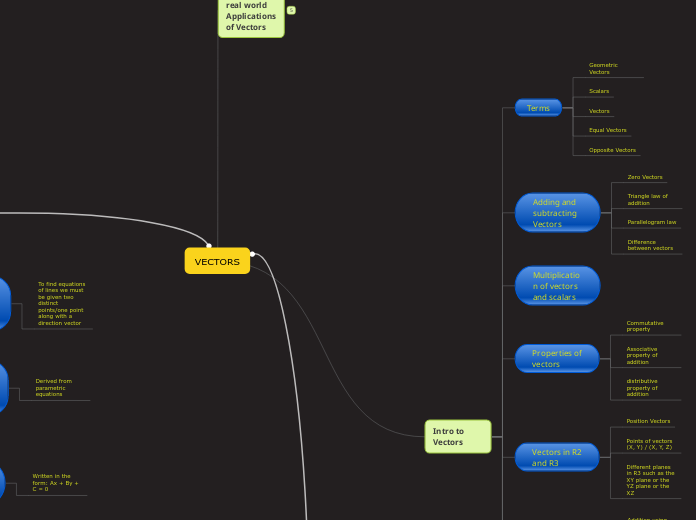
av Hassan Zeeshan 3 år siden
303

Mer som dette
Learn more about how a small village on the banks of the Tiber River became the core of one of the most powerful ancient civilizations.