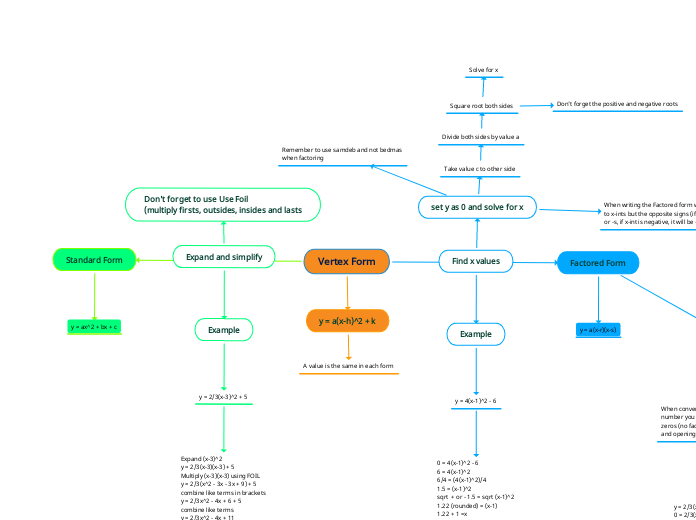
Find x values
y = 4(x-1)^2 - 6
0 = 4(x-1)^2 - 6
6 = 4(x-1)^2
6/4 = (4(x-1)^2)/4
1.5 = (x-1)^2
sqrt + or - 1.5 = sqrt (x-1)^2
1.22 (rounded) = (x-1)
1.22 + 1 =x
x = 2.22
-1.22 = (x-1)
-1.22 + 1 = x
x = -0.22
x ints are = 2.22 and -0.22
y = 4(x-2.22)(x+0.22)
set y as 0 and solve for x
Remember to use samdeb and not bedmas
when factoring
When writing the Factored form with the x-int, r and s are equal to x-ints but the opposite signs (if the x-int is positive,it will be -r or -s, if x-int is negative, it will be +r or +s)
Take value c to other side
Divide both sides by value a
Square root both sides
Don't forget the positive and negative roots
Solve for x
Expand and simplify
y = 2/3(x-3)^2 + 5
Expand (x-3)^2
y = 2/3(x-3)(x-3) + 5
Multiply (x-3)(x-3) using FOIL
y = 2/3(x^2 - 3x - 3x + 9) + 5
combine like terms in brackets
y = 2/3x^2 - 4x + 6 + 5
combine like terms
y = 2/3x^2 - 4x + 11
Don't forget to use Use Foil
(multiply firsts, outsides, insides and lasts
Vertex Form
Standard Form
y = ax^2 + bx + c
Factored Form
Special occasions
When converting from Vertex form to factored form, if the number you are square rooting is negative, then there are no zeros (no factored form). The vertex is either above the x-axis and opening upwards, or it is below and opening downwards.
Example
y = 2/3(x-3)^2 + 5
0 = 2/3(x-3)^2 + 5
-5 = 2/3(x-3)^2
(-5)/(2/3) = (2/3(x-3)^2)/(2/3)
-7.5 = (x-3)^2
cannot square root -7.5, therefore there are no zeros
y = a(x-r)(x-s)
y = a(x-h)^2 + k
A value is the same in each form