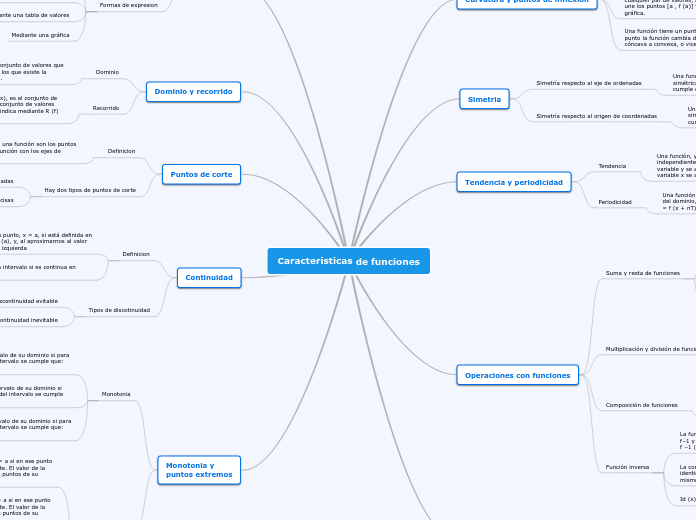
Caracteristicas de funciones

Una función es cóncava en un intervalo de su dominio si, para cualquier par de valores, a y b, del intervalo, el segmento que une los puntos [a , f (a)] y [b , f (b)] queda por debajo de la gráfica.

Una función es convexa en un intervalo de su dominio si, para cualquier par de valores, a y b, del intervalo, el segmento que une los puntos [a , f (a)] y [b , f (b)] queda por encima de la gráfica.

Una función tiene un punto de inflexión en x = a si en ese punto la función cambia de curvatura, es decir, si pasa de ser cóncava a convexa, o viceversa.

Simetría respecto al eje de ordenadas

Una función es simétrica respecto al eje de ordenadas o simétrica par si, para cualquier valor de x de su dominio, se cumple que: f (–x) = f (x)

Simetría respecto al origen de coordenadas

Una función es simétrica respecto al origen de coordenadas o simétrica impar si, para cualquier valor de x de su dominio, se cumple que: f (–x) = –f (x)

Tendencia

Una función, y = f (x), tiende a un valor y0 cuando la variable independiente, x, tiende a un valor x0, si los valores de la variable y se acercan a y0 tanto como se desee cuando la variable x se acerca a x0.

Periodicidad

Una función es periódica, de periodo T, si, para todo valor x del dominio, se cumple que: f (x) = f (x + T) = f (x + 2T) = … = f (x + nT), donde n es un número entero.

Suma y resta de funciones

La suma de las funciones f y g es otra función, f + g, tal que, para cualquier valor de x que pertenezca a los dominios de ambas funciones, se cumple que: (f + g) (x) = f (x) + g (x)

la resta de las funciones f y g es otra función, f – g, tal que, para cualquier valor de x que pertenezca a los dominios de ambas funciones, se cumple que: (f – g) (x) = f (x) – g (x)

Multiplicación y división de funciones

La multiplicación de las funciones f y g es otra función, f · g, tal que, para cualquier valor de x que pertenezca a los dominios de ambas funciones, se cumple que: (f · g) (x) = f (x) · g (x)

La división de las funciones f y g es otra función, image, tal que, para cualquier valor de x que pertenezca a los dominios de ambas funciones y no anule g.

Composición de funciones

La división de las funciones f y g es otra función, image, tal que, para cualquier valor de x que pertenezca a los dominios de ambas funciones y no anule g, se cumple que:

Función inversa

La función inversa o recíproca de la función f se representa por f  –1 y es aquella función que cumple que, si f (x) = y, entonces f   –1 (y) = x.

La composición de dos funciones inversas es la función identidad, es decir, la función que asocia a cada valor consigo mismo:

Id (x) = (f  –1 ∘ f) (x) = x y Id (x) = (f ∘ f  –1) (x) = x

La utilización de funciones es muy habitual a la hora de describir situaciones y fenómenos presentes en nuestra vida cotidiana. El estudio de las características de la función a partir de su representación gráfica permite obtener información de una manera sencilla y clara

Definición

Una función es una relación o correspondencia entre dos variables, x e y, de forma que a cada valor de la variable independiente, x, le corresponde un único valor de la variable dependiente, y.

Formas de expresion

Mediante un enunciado

Mediante una expresión algebraica

Mediante una tabla de valores

Mediante una gráfica

Dominio

El dominio de una función, f (x), es el conjunto de valores que toma la variable independiente, x, para los que existe la función. Se designa por D (f) o Dom (f).

Recorrido

El recorrido o imagen de una función, f (x), es el conjunto de valores que toma la función, es decir, el conjunto de valores que toma la variable dependiente, y. Se indica mediante R (f) o Im (f).

Definicion

Los puntos de corte con los ejes de una función son los puntos de intersección de la gráfica de la función con los ejes de coordenadas

Hay dos tipos de puntos de corte

Punto de corte con el eje de ordenadas

Puntos de corte con el eje de abscisas

Definicion

Una función es continua en un punto, x = a, si está definida en ese punto, es decir, si existe f (a), y, al aproximarnos al valor x = a por su derecha y por su izquierda

Una función es continua en un intervalo si es continua en todos los puntos del intervalo.

Tipos de discotinuidad

Discontinuidad evitable

Discontinuidad inevitable

Monotonia

Una función es creciente en un intervalo de su dominio si para cualquier par de valores, a y b, del intervalo se cumple que: si a < b ⇒ f (a) ≤ f (b)

Una función es decreciente en un intervalo de su dominio si para cualquier par de valores, a y b, del intervalo se cumple que: si a < b ⇒ f (a) ≥ f (b)

Una función es constante en un intervalo de su dominio si para cualquier par de valores, a y b, del intervalo se cumple que: si a < b ⇒ f (a) = f (b)

Puntos extremos

Una función tiene un máximo relativo en x = a si en ese punto la función pasa de ser creciente a decreciente. El valor de la imagen de x = a, f (a), es mayor que en los puntos de su entorno.

Una función tiene un mínimo relativo en x = a si en ese punto la función pasa de ser decreciente a creciente. El valor de la imagen de x = a, f (a), es menor que en los puntos de su entorno.

Una función tiene un máximo absoluto en x = a si su imagen, f (a), es mayor o igual que el valor de la función en cualquier otro punto de su dominio:

Una función tiene un mínimo absoluto en x = a si su imagen, f (a), es menor o igual que el valor de la función en cualquier otro punto de su dominio: