Estadística
Origen
s. XVI
Cens
Exposició ordenada
s. XVII - s. XIX
Anàlisi de dades
Treure conclusions
finals s. XIX
Inferencial
Extreure conclusions per validar tota la població
Tipus
Descriptiva
Exposa i analitza dades d'un grup donat
No extraiem conclusions sobre un grup més ampli
Inferencial
Treballa amb mostres
Inferim les característiques obtingudes a tota la població
Etapes Estudi
Identificar població
Identificar variable/s a estudiar
Identificar tècnica de mostreig
Dissenyar recollida de dades
Organitzar en taules
Analitzar dades recollides
Paràmetres numèrics
Representació Gràfica
Recollida de dades
Fonts
Enquestes
Experiments
Cens
Població
Objecte de l'estudi
Mida de la població = N
Element o individu
Mostra
Subconjunt representatiu de la població per estudiar i inferenciar
Mida de la mostra = n
Testimoni: Individu mostra
Tècniques de mostreig
Aleatori
Simple
Sistemàtic
Primer aleatori
Següents: k=N/n
Estratificat
Mateixa proporció que la població
Biaix
Mostreig aleatori total
No Aleatori
Selectiu
Característiques concretes
Local
Entorn o zona concreta
en Cadena
Vincles amb el testimoni anterior
Tipus de dades
Variables estadístiques
Qualitatives
Categories o atribut
Ordenades
Dia setmana
Any
Formatge preferit
Mes de l'any
No ordenades
Color d'ulls
Continent origen
Quantitatives
S'expressen numèricament
Discretes
Nombre finit de valors, enters
Número PC
Número TV
Número de peu
Habitants
Continues
Qualsevol valor d'un interval
Pes
Altura
Velocitat
Ingressos mensuals
Qualitatives
Diagrama de sectors

Añada su texto
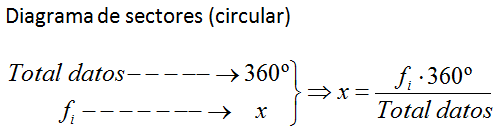
Añada su texto
Observem freqüències relatives (no absolutes)
Diagrama de barres

Añada su texto
Longitud proporcional a la freqüència
Comparar freqüència absoluta
Gràfic de línies
Añada su texto
No per observar freqüències
És per observar la relació que mantenen dues variables inddependents
Quantitatives
Discretes
Diagrama de barres

Añada su texto
Longitud proporcional a la freqüència
Comparar freqüència absoluta
Diagrama de sectors
Gràfic de línies
Continues
Han de ser segmentades en intervals, no hi ha separació entre les barres
Histogrames
Añada su texto
Comparar freqüència absoluta
Piràmides de població

Añada su texto
Comparar freqüència absoluta de 2 variables
Polígon de freqüències

Añada su texto
Recompte de dades
Per categories
Dades qualitatives o quantitatives discretes amb dades que es repeteixen sovint
Poques dades

Taula de freqüències
Variable = Xi
Variables estadístiques de l'estudi
Freqüència Absoluta = fi
Nombre de vegades que es repeteix les variables
Freqüència Absoluta Acumulada = Fi
Freqüència Relativa = hi = ni
Añada su texto
Freqüència Relativa Acumulada = Hi = Ni
Per intervals
Dades quantitatives discretes o continues amb dades que NO es repeteixen sovint les classes es defineixen per intervals
Moltes dades
Dades agrupades per intervals o classes
Exemple:
Mateixa amplitud
Mínim 4
Punt mitjà interval: Marca de classe
Gràficament:
Histogrames
Alçada: Proporcional a la freqüència
Amplada: Interval
Polígon freqüències
Línia que uneix extrems superiors barres
Probabilitat
Llenguatge
Determinista
Experiments no aleatoris
Experiència aleatòria
No coneixem els resultats i cada cop Diferents resultats
Llançament dau
Espai mostral
Conjunt de tots els possibles esdeveniments que es poden donar
E={1, 2, 3, 4, 5, 6}
Esdeveniment (A, B, C, ...)
Conjunt format per un o diversoso resultats possibles
A=(Treure un nombre primer)={2, 3, 5}
B=(Treure un nombre parell)={2, 4, 6}
Resultats favorables
Tipus
Elemental
Un sol element de l'experiment
Compost
Varis successos elementals
Segur
Esdeveniment que sempre té lloc, format per tots els esdeveniments = Espai mostral
B=(Treure un nombre < o = 6) = {1, 2, 3, 4, 5, 6}
Impossible
Mai passa = conjunt buit
B = (Treure un nombre 6< ) = {Conjunt buit}
Contrari a un esdeveniment A
A' = (NO Treure un nombre primer)={1, 4, 6}
Compatibles
Tenen resultats favorables en comú
Incompatibles
Dos successos que no poden tenir lloc al mateix moment i no tenen cap element en comú
Operacions amb esdeveniments
Llenguatge de conjunts
Añada su texto
Unió
Resultats favorables

Añada su texto
Intersecció
Resultats favorables a tots dos alhora
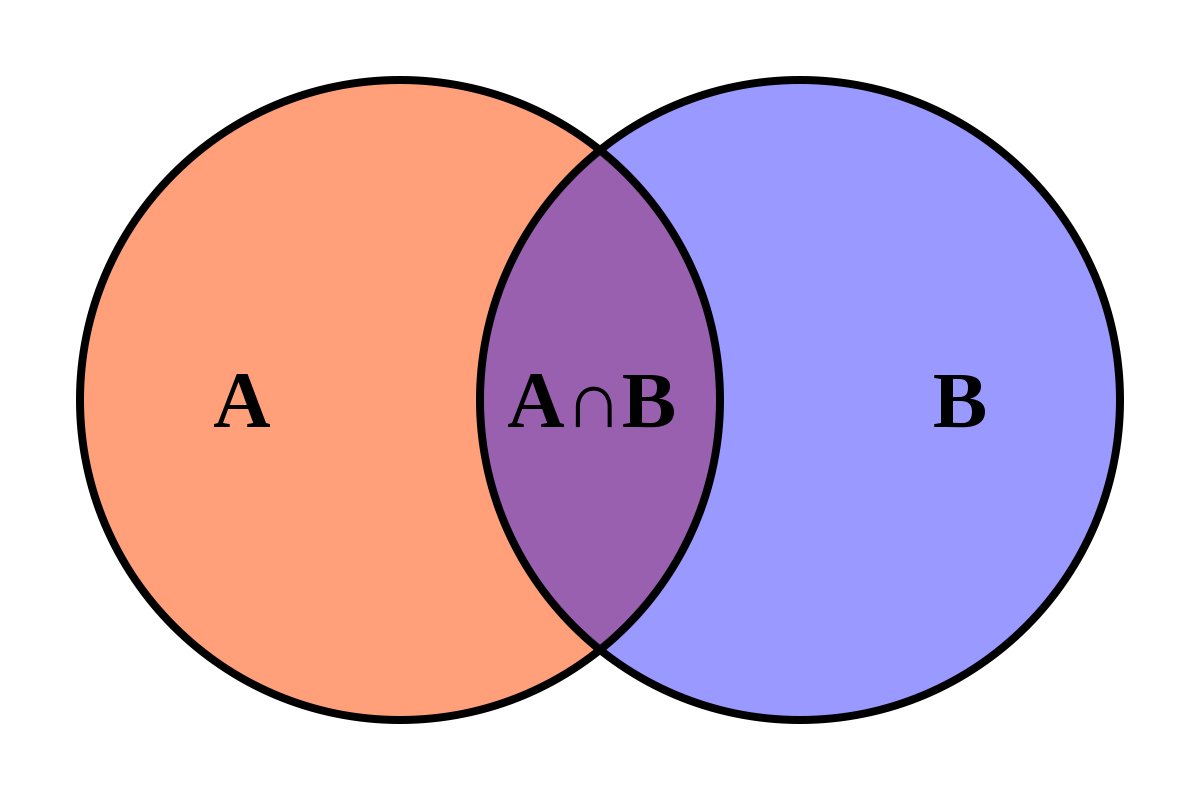
Añada su texto
Añada su texto
Contrari

Añada su texto
Freqüències
Absoluta: f(A)
Vegades que s'obté succés repetint N vegades experiment
Relativa: h(A)
h(A) = f(A)/N
Valor entre 0 i 1
h(E)= 0 --> Esdeveniment Impossible
h(E)= 1 --> Esdeveniment Segur
Incompatibles
h(AuB) = h(A) + h(B)
Compatibles
h(AuB) = h(A) + h(B) -h(AiB)
Probabilitat
Repetim esdeveniment--> Freqüència relativa s'acosta a un valor fix anomenat PROBABILITAT
Possibilitats de que tingui lloc l'esdeveniment = P(A)
P(A) entre 0 i 1
Impossible
P(A)=0
Segur
P(A)=1
P(AuA') = P(A) + P(A') = 1
Contrari
P(A') = 1- P(A)
Unió
Incompatibles
P(AuB) = P(A) + P(B)
Compatibles
P(AuB) = P(A) + P(B) - P(AiB)
Compost
Suma de les probabilitats dels esdeveniments elementals
Regla de Laplace
Resultats possibles: Equiprobables, mateixa probabilitat
Añada su texto
Bidimensional
Distribucions bidimensionals
2 variables: x, y
Taula de contingència
Taula de freqüències conjuntes de dues variables
Simple

Añada su texto
Doble entrada

Añada su texto
Freqüències marginals
Valors independents

Añada su texto
Mesures marginals
Gràficament
Diagrama de dispersió o núvol de punts
Añada su texto
Punt: (x, y)
Correlació lineal
relació entre les variables
Núvol s'acosta a la recta (funció)
Més aprop més correlació
Coeficient de correlació de Pearson

Añada su texto
Mesures de dispersió
Indiquen si les dades estan més o menys agrupades respecte de les mesures de centralització
Rang

Añada su texto
Desviació mitjana

Añada su texto
Variància
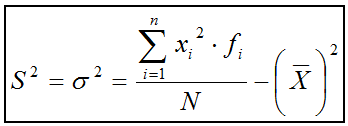
Añada su texto
A més gran dades més disperses
Desviació típica
Añada su texto
A més gran dades més disperses
Coeficient de variació

Añada su texto
Comparar les dispersions de dades de diferent mitjana
Quan més baix més homogènia la distribució
Distribució normal
Fenòmens relacionats amb la naturalesa i els éssers vius

Añada su texto
Gràficament
Añada su texto

Añada su texto
Reflecteix gràficament la dispersió de les dades
Añada su texto
Mesures de posició
Añada su texto
Ordenem les dades
Percentils
Partim la població
P30=30%
P10=10%
P80=80%
Quartils
Partim la població
Q1=25%
Q2=50%
Q3=75%
Mitjana

Añada su texto
Añada su texto
Moda (Mo)
Observació que més es repeteix
Añada su texto
Mediana (Me)
Mostra parell
Mitjana de les dues dades centrals
Añada su texto
Mostra imparell
Posició central

Añada su texto
Diagrama de caixa i bigotis

Añada su texto
Representar distribucions
Ordenar dades
Valors mínim i màxim
Quartils
Mediana
Eix abscicsses
Recorregut interquartílic
Q3-Q1
Paràmetres freqüència
Freqüència absoluta: fi
Freqüència absoluta acumulada: Fi
Freqüència relativa: hi
Freqüència relativa absoluta: Hi
Paràmetres Classe
Intervals de classe o Classe: Ci
Nombre de classes: Nc = Part sencera (arrel N)
Amplitud de classe: Ac = Ar/Nc
Rang de classe: Rc:[Vcmin; Vcmax)
Marca de classe: Ci (mitjana)
Paràmetres generals
Mida població: N
Mida de la mostra: n
Valor mínim: Vmin
Valor màxim: Vmax
Rang: R:[Vmin;Vmax]
Amplitud del rang: Ar=Vmax-Vmin
Paràmetres
Valor representatiu d'una població
Generals
Mesures de posició
Centrals
No Centrals
Mesures de dispersió
Absolutes
Relatives
Altres