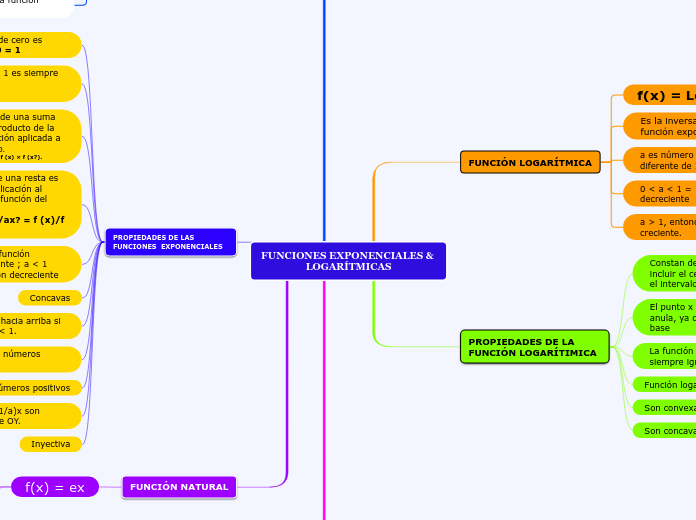
FUNCIONES EXPONENCIALES & LOGARÍTMICAS

f(x) = Log ax

Es la inversa de la función exponencial

a es número real positivo, a > 0, y diferente de 1, a ≠ 1.

0 < a < 1 = función logarítmica decreciente

a > 1, entonces es una función creciente.

Constan de valores de x positivos, sin incluir el cero. Por tanto, su dominio es el intervalo (0,+infinito)

El punto x = 1, la función logarítmica se anula, ya que loga 1 = 0, en cualquier base

La función logarítmica de la base es siempre igual a 1

Función logarítmica es continua

Son convexas si a > 1

Son concavas si 0 < a < 1 .

Una función exponencial es aquella que la variable independiente "x" aparece en el exponente y tiene de base una constante a

f(x)= a^x

Se considera la inversa de la función logarítmica

Función aplicada el valor de cero es igual a 1 f (0) = a^0 = 1

La función exponencial de 1 es siempre igual a la base:
f (1) = a1 = a.

La función exponencial de una suma de valores es igual al producto de la aplicación de dicha función aplicada a cada valor por separado.
f (x + x?) = ax+x? = ax × ax? = f (x) × f (x?).

La función exponencial de una resta es igual al cociente de su aplicación al minuendo dividida por la función del sustraendo:
f (x - x?) = ax-x? = ax/ax? = f (x)/f (x?).

a >1 función creciente ; a < 1 función decreciente

Concavas

La curva es cóncava hacia arriba si : b>1 y cuando 0<b< 1.

El dominio consiste en los números reales

Rango: Números positivos

Las curvas y = ax e y = (1/a)x son simétricas respecto del eje OY.

Inyectiva

f(x) = ex

Dominio: numeros reales

Recorrido: Im(f) = R

Si es creciente su curva es cóncava hacia arriba

convexas

a>1 = x → 0 + , entonces log a x → - ∞

0<a<1=x → 0 + , entonces log a x → + ∞