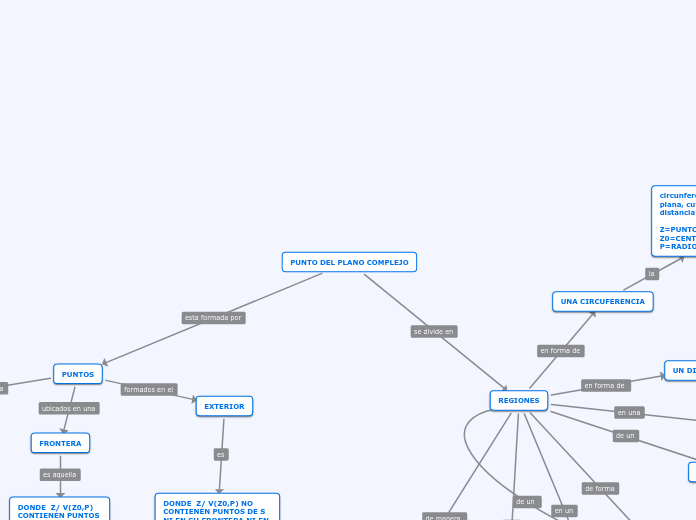
PUNTO DEL PLANO COMPLEJO
PUNTOS
INTERIOR
TODOS AQUELLOS
PUNTOS Z0 CONTIENEN
UNA VECINDAD.
|Z||˂P
|Z-Z0||˂P
TOTALMENTE CONTENIDO EN
EN S.
EXTERIOR
DONDE Z/ V(Z0,P) NO
CONTIENEN PUNTOS DE S
NI EN SU FRONTERA NI EN
SU INTERIOR.
FRONTERA
DONDE Z/ V(Z0,P)
CONTIENEN PUNTOS
DENTRO Y FUERA DE
LA REGION S
REGIONES
UN DISCO
cuando su conjuto S esta conformado por
puntos interiores,puntos fronteras y ademas de esto esta formado por puntos
exteriores.
VECINDAD
Como vecindad del punto Z0, que está en el plano complejo, a todo conjunto V que contiene un círculo abierto
V(Z0,P) = {z / |z-Z0 | < P},
de centro Z0 y radio P> 0.
El círculo V(Z0,P ) es, obviamente, una vecindad de Z0
SE CONFORMA EN DOS
VECIDAD COMPLEJA
De la forma |Z-Z0||˂P
VECINDAD
De la forma 0<|Z-Z0||˂P
CONJUTO ABIERTO
que es un conjunto abierto cuando
cada unos de los puntos S de un conjunto
es un punto interior.
UNA CIRCUFERENCIA
circunferencia es una línea curva, cerrada y plana, cuyos puntos están todos a la misma distancia de otro punto, llamado centro.
|Z-Z0||=P
Z=PUNTOS DE LA CIRCUFERENCIA
Z0=CENTRO DE LA CIRCUFERENCIA
P=RADIO.
CONJUNTO CERRADO
Cuando el conjunto S contiene puntos
interior y puntos frontera.
CONVEXA
como conjunto conexo, cuando en el conjuto S los puntos que la conforman se pueden conectar mediante una linae recta
poligonal que consite en un numero finito
de segmentos.
DOMINIO
Subtopic
ACOTAMIEMTO
existe una sierta vecindad del origen
que encierra totalmente a S.
INFINITO
Los conjuntos finitos tienen una propiedad "intuitiva" que los caracteriza: "dada una parte propia de los mismos, esta contiene un número de elementos menor que todo el conjunto". Es decir, no puede establecerse una biyección entre una parte propia del conjunto finito y todo el conjunto
Técnicamente es la proyección estereográfica de los números complejos ampliados con el ∞, donde se define una nueva distancia para obtener una topología. Lo que tiene aplicaciones en geometría algebraica, teoría de la relatividad o mecánica cuántica y sirve para visualizar la 4ª dimensión