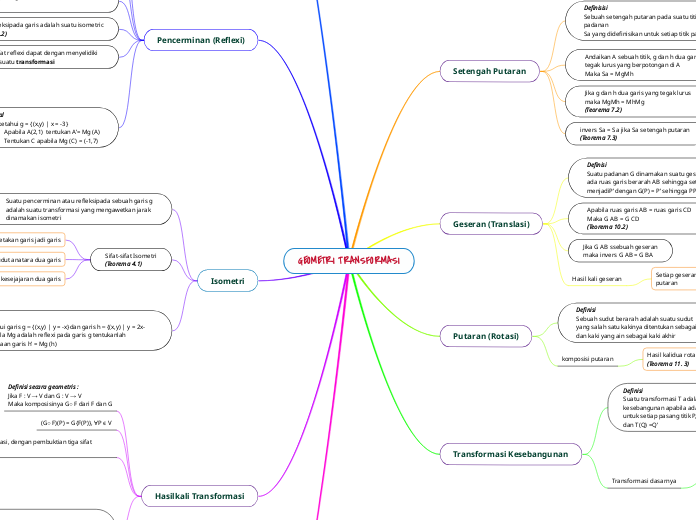
GEOMETRI TRANSFORMASI
Setengah Putaran
Definisisi
Sebuah setengah putaran pada suatu titik A adalah suatu padanan
Sa yang didefinisikan untuk setiap titik pada bidang
Apabila P ≠ A maka Sa (P) = P
Sehingga A titik tengah ruas garis PP’
Sa (A) = A
Andaikan A sebuah titik, g dan h dua garis
tegak lurus yang berpotongan di A
Maka Sa = MgMh
Jika g dan h dua garis yang tegak lurus
maka MgMh = MhMg
(Teorema 7.2)
invers Sa = Sa jika Sa setengah putaran
(Teorema 7.3)
Geseran (Translasi)
Definisi
Suatu padanan G dinamakan suatu geseran apabila
ada ruas garis berarah AB sehingga setiap titik P pada bidang
menjadiP’ dengan G(P) = P’ sehingga PP’ = AB
Apabila ruas garis AB = ruas garis CD
Maka G AB = G CD
(Teorema 10.2)
Jika G AB ssebuah geseran
maka invers G AB = G BA
Hasil kali geseran
Setiap geseran dapat diuraikan sebagai hasi kalidua setengah putaran
Putaran (Rotasi)
Definisi
Sebuah sudut berarah adalah suatu sudut
yang salah satu kakinya ditentukan sebagai kaki awal
dan kaki yang ain sebagai kaki akhir
komposisi putaran
Hasil kalidua rotasi adalah sebuah rotasi atau sebuah translasi
(Teorema 11. 3)
Transformasi Kesebangunan
Definisi
Suatu transformasi T adalah suatu transformasi kesebangunan apabila ada sebuah konstanta k>0 sehingga untuk setiap pasang titik P,Q, jarak P’Q’ = KPQ dengan T(P) = P’ dan T(Q) =Q’
Isometri, jika k =1
Transformasi dasarnya
Dilasi
Definisi
Diketahui sebuah titik A dan sebuah bilangan positif k. Suatu dilasiD dengan faktor skala k dan pusat A adalah padanan
• D(A) = A
• P ≠ A, D(P) = P’ adalah titik tengah sinar AP Sehingga AP’ = k(AP)
Hasil kalidua dilasi adalah dilasi
(Teorema 14.3
Transformasi
f : V → V
Tiga sifat Transformasi
Injektif
Jika A1 ≠ A2
T(A1) = B1, T(A2) = B2
Maka B1 ≠ B2
Surjektif
Pada B ϵ V
Ada A ϵ V
Sehingga B = T (A)
Bijektif
Jika Surjektif dan Injektif
Soal :
Andaikan g dan h dua garis yang sejajar pada bidang Euclides V. A sebuah titik yang terletak ditengah antara g dan h. Sebuah T padanan dengan daerah asal g yang didefinisikan sebagai berikut :
Apabila P ϵ g maka P’ = T(P) = PA Ո h
a. Apakah daerah nilai T ?
b. Apakah T injektif ?
Jawab :
a) Daerah nilai T adalah garis h
b) Akan dibuktikan T injektif
Ambil dua titik X dan Y pada g, dengan X ≠ Y. Akan ditunjukkan bahwa T(X) ≠ T(Y) dengan menggunakan kontradiksi.
Andaikan T(X) = T(Y), sehingga haruslah X = Y, hal ini menghasilkan kontradiksi, sebab awalnya dikatakan X ≠ Y. jadi pengendaian di ingkari. Dengan demikian, T(X) ≠ T(Y) dan dapat disimpulkan bahwa T injektif (Terbukti)
Pencerminan (Reflexi)
Definisi secara geometris
Sebuah garis s adalah fungsi Ms untuk setiap titik pada bidang
Jika P ϵ s, maka Ms (P) = P
Jika P ∉ s, maka MS
Sehingga garis s adalah sumbu ruas garis PP’
Secara umum
Refleksi merupakan transformasi berupa pemindahan setiap titik pada objek geometri melewati sebuah cermin (sumbu)
Setiap refleksipada garis adalah suatu transformasi
(Teorema 3.1)
Setiap refleksipada garis adalah suatu isometric
(Teorema 3.2)
Untuk menyelidiki sifat-sifat reflexi dapat dengan menyelidiki apakah pencerminan itu suatu transformasi
Soal
Diketahui g = {(x,y) | x = -3}
a. Apabila A(2,1) tentukan A’= Mg (A)
b. Tentukan C apabila Mg (C) = (-1,7)
Jawab :
a) g : x = -3 melalui A(2,1), y = 1. B(-3,1)
(-3,1) = ((x_A+ x_A' )/2,(y_A+y_A')/2)
= ((2+ x_(A^' ) )/2,(1+y_A')/2)
(-6,2) = (2+ x_(A^' ) ,1+y_A')
(xA’ , yA’) = (-8,1)
b) y = 7, titik D(-3,7)
(-3,7) = ((x_c+ x_c' )/2,(y_c+y_c')/2)
= ((x_c-1 )/2,(y_c+7)/2)
(-6,14) = (x_c-1,y_c+7)
(xc’ , yc’) = (-5,7)
Isometri
Suatu pencerminan atau refleksipada sebuah garis g
adalah suatu transformasi yang mengawetkan jarak
dinamakan isometri
Sifat-sifat Isometri
(Teorema 4.1)
Memetakan garis jadi garis
Mengawetkan sudut anatara dua garis
Mengawetkan kesejajaran dua garis
Soal
Diketahui garis g ≡ {(x,y) | y = -x}dan garis h ≡ {(x,y) | y = 2x-3}apabila Mg adalah reflexi pada garis g tentukanlah persamaan garis h’ = Mg (h)
Jawab :
Karena Mg adalah sebuah reflexi pada gjadi suatu isometri, maka menurut teorema 4.1, h’ adalah sebuah garis.
Garis h’ akan melalui titik potong antara h dan g, misalnya R, sebab Mg (R) = R.
Jelas bahwa R(1,-1) : hakan melalui Q’ = Mg (Q).
Karena Q = (3/2 , 0) maka Q’ = (0, -3/2)
Sehingga persamaan h’ adalah h’ = {(x,y) | x-2y-3 = 0}
Hasilkali Transformasi
Definisi secara geometris :
Jika F : V → V dan G : V → V
Maka komposisinya G○ F dari F dan G
(G○ F)(P) = G{F(P)}, ⱯP ϵ V
Merupakan Transformasi, dengan pembuktian tiga sifat transformasi
Soal
Diketahui h adalah sumbu –x dan g adalah sumbu –y sebuah sumbu sistem orthogonal. Diketahui A(4,-3) dan P(x,y). Tentukanlah :
a. Koordinat-koordinat MhMg (A) dan MgMh (A)
b. Koordinat-koordinat MhMg (P)
a. Koordinat-koordinat MhMg (A)
MhMg (A) = Mh [Mg (A)]
= Mh [Mg (4,-3)]
= Mh (-4,-3)
= (-4,3)
Koordinat-koordinat MgMh (A)
MgMh (A) = Mg [Mh (A)]
= Mg [Mh (4,-3)]
= Mg (-4,-3)
= (-4,3)
b. Koordinat-koordinat MhMg (P)
MhMg (P) = Mh [Mg (P)]
= Mh [Mg (x,y)]
= Mh (-x,y)
= (-x,-y)
Transformasi Balikan
Definisi secara geometris
Setiap transformasi T memilikibalikan (invers)
(Teorema 6.1)
TI = IT = T
Setiap transformasimemiliki hanya satu balikan
Teorema (6.2)
Balikan setiap pencerminan pada garis adalah pencerminan itu sendiri
Teorema (6.3)
Involusi
balikan transformasi adalah dirinya sendiri
Soal
Jika g sebuah garis dan A sebuah titik, tenukan baliakan transformasi Wg :
Jawab :
A ϵ g, jjika A ϵ V, maka IA = A
IA = A
[Wg-1. Wg](A) = A
Wg-1[ Wg(A)] = A
Wg-1(A) = A
A bukan ϵ g, maka Wg (A)= A’ = ½ h = ½ A
h tegak lurus g dari A
Maka, Wg-1(A) = Vg(A)