Development of mathematical limit through the history
Zeno of Elea (495-425 b.C)

Zeno's paradox Achilles and the tortoise
In the paradox of Achilles and the tortoise, Achilles is in a footrace with the tortoise. Achilles allows the tortoise a head start of 100 meters, for example. Supposing that each racer starts running at some constant speed (one very fast and one very slow), then after some finite time, Achilles will have run 100 meters, bringing him to the tortoise's starting point. During this time, the tortoise has run a much shorter distance, say, 10 meters. It will then take Achilles some further time to run that distance, by which time the tortoise will have advanced farther; and then more time still to reach this third point, while the tortoise moves ahead. Thus, whenever Achilles arrives somewhere the tortoise has been, he still has some distance to go before he can even reach the tortoise

Democritus of Abdera (460-370 b.C)

Democritus was great when he imagined that the volume of a cone or a pyramid could be achieved by calculating separately the volume of the different superimposed thin sheets in which the aforementioned geometric solids had been subdivided.
Aristotle of Stagira (384-322 b.C)

distinguished actual and potential infinity, but mathematical infinity, in Aristotle’s opinion, is merely potential (he, avoiding paradoxes, refused actual infinity: Bostock, 1972-1973). As regards infinitesimal, according to the concept of number line, the ancient conception is only potential, although interesting ideas can
be related to the exhaustion argument
Archimedes of Syracuse (287– 212 b.C)

he was the first developing the idea of limits to measure curved figures and the volume of a sphere in the third century B.C. By carving these figures into small pieces that can be approximated, then increasing the number of pieces, the limit of the sum of pieces can give the desired quantity

Topic principal
Topic principal
Topic principal
Subtema
Topic principal
Topic principal
Limit, mathematical concept based on the idea of closeness, used primarily to assign values to certain functions at points where no values are defined, in such a way as to be consistent with nearby values.
John Wallis

John Wallis was a mathematical Englishman who is given partial credit for the development of infinitesimal calculus and him was the first to clearly establish the notion of limit in the rigorous form in force today. It was he who introduced the symbol ∞, which is currently used to represent a countless number, that is, infinite. He also published a work called Arithmetica Infinitorum, where he expanded and systematized the methods of analysis of Descartes and Cavalieri. Developed a standard notation for powers, extending it from positive integers to rational numbers.
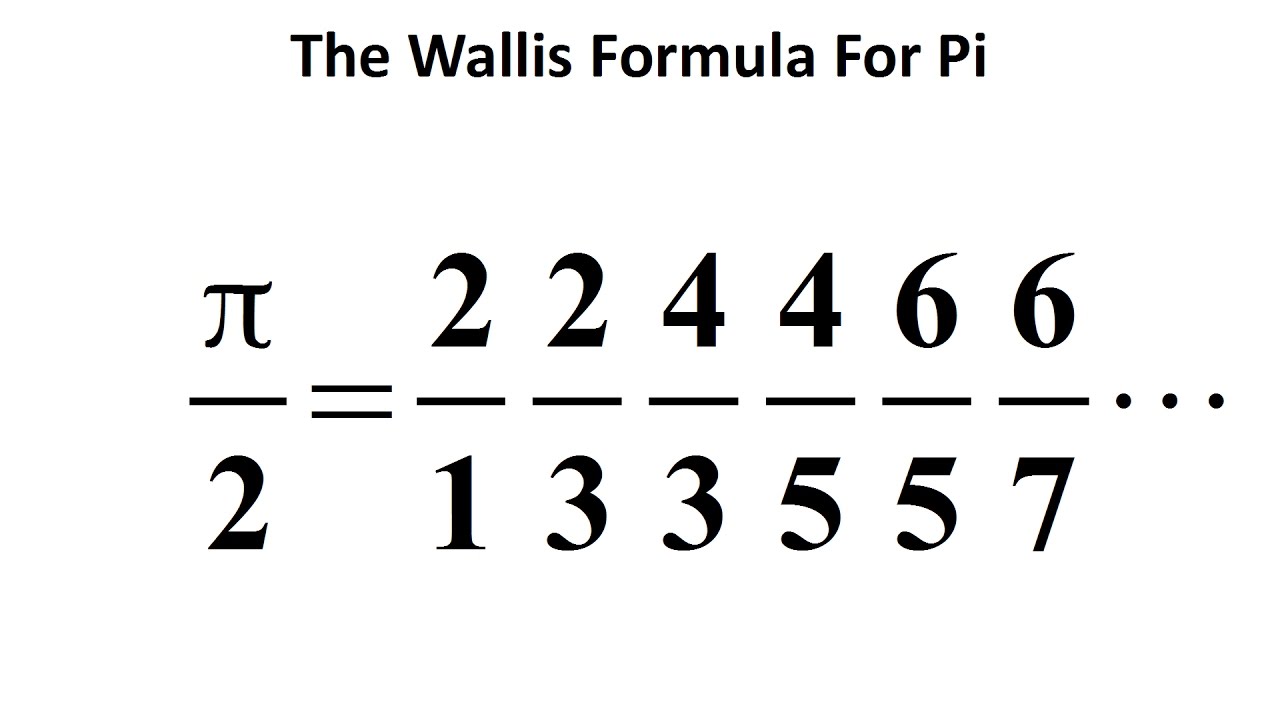
A few years later, in 1659, Wallis published a tract containing the solution of the problems on the cycloid which had been proposed by Blaise Pascal. In this he incidentally explained how the principles laid down in his Arithmetica Infinitorum could be used for the rectification of algebraic curves and gave a solution of the problem to rectify (i.e., find the length of) the semicubical parabola x3 = ay2, which had been discovered in 1657 by his pupil William Neile.