Probabilidad: Conceptos básicos
Experimento Aleatorio
Es aquel experimento que no presenta siempre el mismo resultado, de hecho, no se puede predecir el resultado.
Ejemplos

Lanzar un dado equilibrado
Número de accidentes automovilísticos en un día

Comprar un boleto de lotería
Espacio Muestral
Es el conjunto de todos los resultados posibles de un experimento aleatorio y son finitos. Se suele representar con S
Ejemplos
Lanzar un dado equilibrado: S = {1,2,3,4,5,6}
Número de accidentes automovilísticos en un día: S = {t l t ∈ [0,n)}
Comprar un boleto de lotería: S= {0,1}
Un evento es un subespacio del espacio muestral, es decir, contiene resultados que están dentro del espacio muestral, entonces siempre son menos o iguales a los del espacio muestral, se suele representar con una letra mayúscula
Ejemplos
Obtener un 3 al lanzar un dado: A = {3}

Que haya menos de 100 accidentes automovilísticos en un día B = {t l t<100}

Ganar la lotería C = {1}
Probabilidad de un evento
La probabilidad de un evento siempre está en entre 0 y 1, siendo la probabilidad 0 el hecho de que no puede ocurrir y 1 el hecho de que definitivamente va a ocurrir.
Probabilidad frecuentista y subjetiva

Frecuentista: Si definimos nA como el numero de veces que ocurrió el evento A en n repeticiones de un experimento aleatorio entonces P(A)=límite cuando n tiende a infinito de (nA/n), mediante esta definición no es posible encontrar la probabilidad exacta, el resultado es una aproximación empírica.
Subjetiva: Esta probabilidad depende de lo que el observador conozca del fenómeno, se le puede considerar informal pero a veces resulta necesario recurrir a ella. Se suele solicitar a un experto para determinar si la probabilidad es alta o baja.
Probabilidad geométrica
Si un experimento aleatorio tiene como espacio muestral 𝑆 ⊂ ℝ2 y su área está definida concretamente entonces P(A)= Área de A/ Área de S
Postulados
1.- P(A)≥0
2.- 𝑃(S)= 1
3.- Si A1 A2, ... son eventos finitos o infinitos mutuamente excluyentes en S entonces P(A1 u A2 u A3...) = P(A1)+P(A2)+...
Probabilidad clásica

Sea A un evento (subconjunto) del espacio muestral S entonces la probabilidad clásica del evento es: P(A)= #A/#S, donde #A y #S representa el número de elementos que contiene cada conjunto. Nota: S debe ser equiprobable
Postulados
1.- P(A)≥0
2.- 𝑃(S)= 1
3.- Si A1 A2, ... son eventos finitos o infinitos mutuamente excluyentes en S entonces P(A1 u A2 u A3...) = P(A1)+P(A2)+...
Probabilidad axiomatica
Aquí es donde se proponen las reglas del cálculo de probabilidades, no se pretende calcularlas explícitamente.
Propiedades
P(A)>0
P(S)=1
(No se puede escribir la fórmula) 3.- La probabilidad de la unión infinita de eventos Ai ajenos dos a dos es la suma de todas y cada una de las probabilidades de Ai
P(∅ )=0
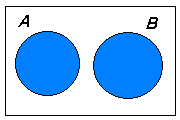
P(A U B)= P(A)+P(B) cuando P(A∩B)=0
Para cualquier evento A, P(A)=1-P(Ac)
𝐴 ⊆ 𝐵 entonces P(A)≤ P(B).
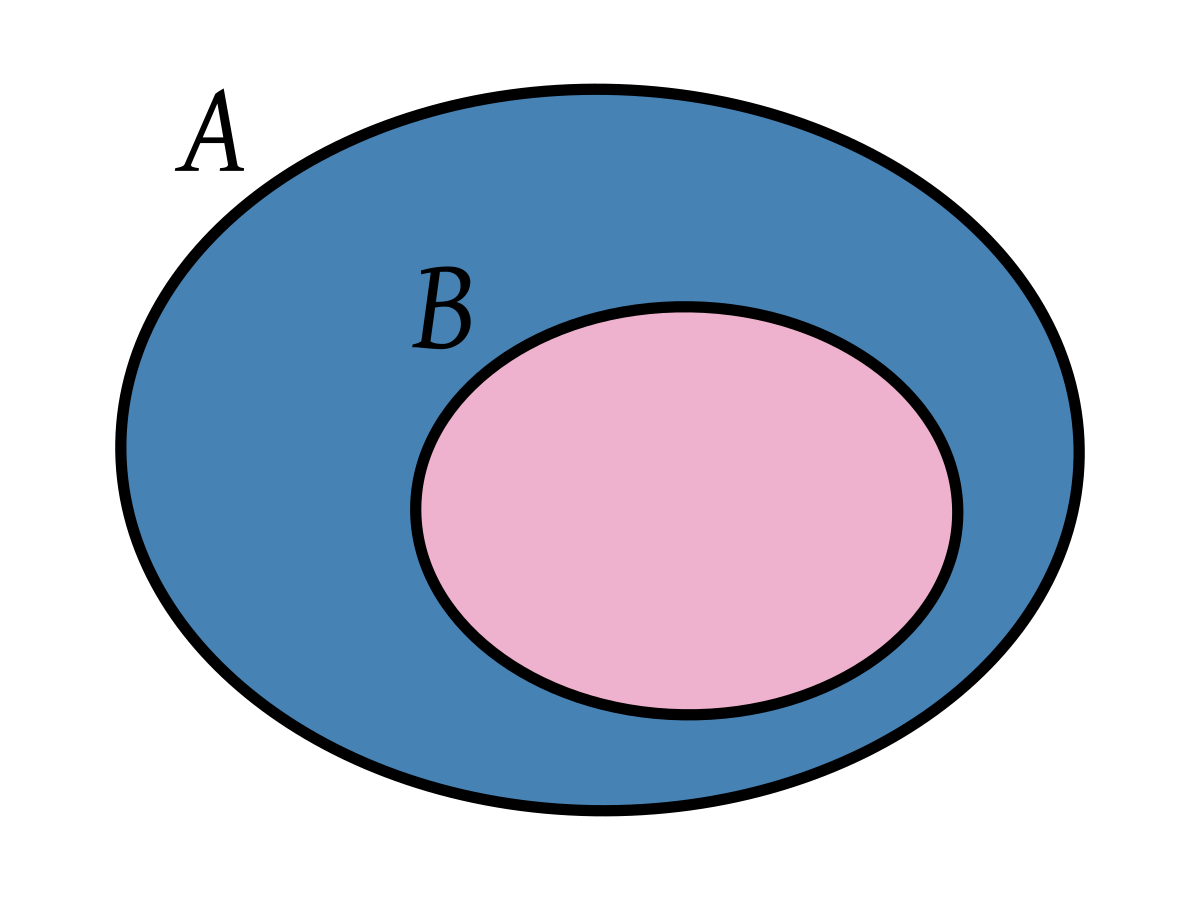
Si 𝐴 ⊆ 𝐵 entonces 𝑃(𝐵 − 𝐴) = 𝑃 (𝐵) − 𝑃(𝐴)
Para cualquier evento A, 0 ≤ 𝑃(𝐴) ≤ 1
Para cualesquiera eventos A y B, 𝑃(𝐴 ∪ 𝐵) = 𝑃(𝐴) + 𝑃(𝐵)− 𝑃(𝐴∩ 𝐵).
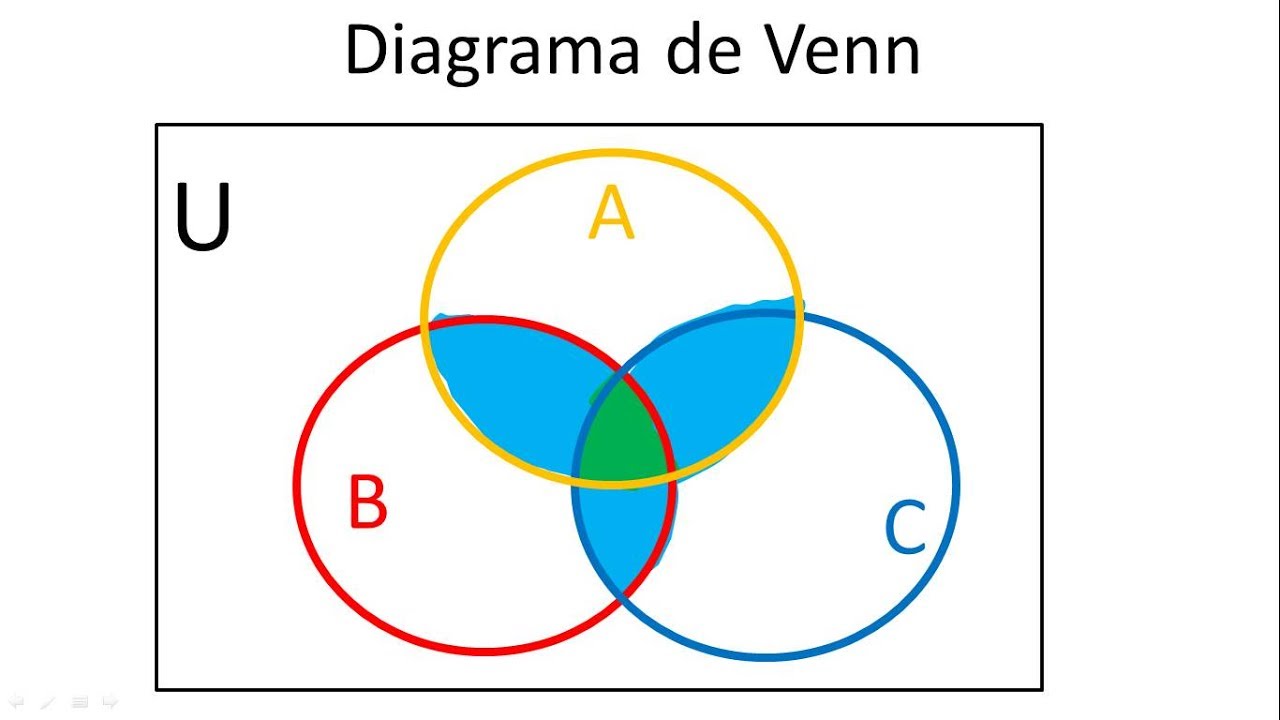
Para cualesquiera eventos A, B Y C, 𝑃(𝐴∪𝐵∪𝐶)= 𝑃(𝐴)+𝑃(𝐵)+𝑃(𝐶)−𝑃 (𝐴 ∩ 𝐵)−𝑃(𝐴 ∩ 𝐶) −𝑃(𝐵 ∩ 𝐶)+ 𝑃(𝐴 ∩ 𝐵 ∩ 𝐶)
Probabilidad condicional
La probabilidad condicional se utiliza cuando se quiere calcular la probabilidad de un evento que comparte elementos con otros eventos.

Sean dos eventos A y B, la probabilidad condicional de A dado B se denota por: P(A l B)= P(AnB)/P(B). En esta probabilidad se tiene por hecho que B ha ocurrido, por lo que todo lo que esté fuera de B tiene probabilidad 0, y evidentemente si A y B no tienen intersecciones entonces la probabilidad condicional será de 0.
Propiedades
𝑃(𝐴|𝐵)≥ 0
𝑃(𝑆|𝐵)=1
𝑃(𝐴1∪𝐴2|𝐵) = 𝑃(𝐴1)+𝑃(𝐴2) cuando A1 Y A2 son ajenos
Teorema de Bayes
Este teorema hace uso de la probabilidad total, calcula lo de la probabilidad total pero en el sentido contrario, es decir, se calcula la probabilidad de que ocurra B dado que ocurrió algún evento A, tiene un papel muy importante en la teoría de probabilidad
Sea B1, B2, B3,...,Bn tal que P(Bi)≠0, i=1,2,...,n y sea A un evento tal que P(A)≠0 entonces para cada j=1,2,3...n P(Bj l A)= P(A l Bj)P(Bj)/[P(A l B1)P(B1)+...+P(A l Bi)P(Bi)]
Probabilidad total

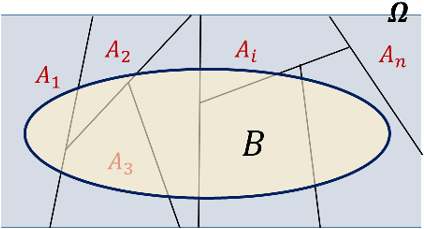
En esta probabilidad se hace uso de la probabilidad condicional, como el espacio muestral está totalmente repartido entre eventos A y tenemos un evento B que comparte elementos con algunos eventos A entonces resulta muy útil como esta fórmula calcula la probabilidad de que haya ocurrido un evento A dado que ocurrió B.
Sean A1, A2,..., An eventos, son una partición finita de S si
A𝑖 ≠ ∅ para 𝑖 = 1, … ,n
A𝑖 ∩ A𝑗 = ∅ para 𝑖 ≠ j
Sea A1, A2,..., An una partición de S tal que P(Ai) ≠ 0. Para cualquier evento B, P(B)=P(B l A1)P(A1)+P(B l A2)P(A2)+...+P(B l An)P(An)
La unión de todos los eventos Ai = S
Independencia de eventos
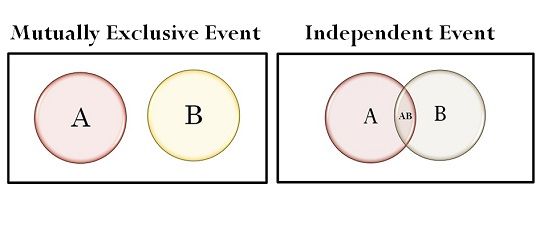
La independencia de eventos se da cuando la ocurrencia de un evento no afecta la probabilidad de que ocurra otro.
Se dice que A y B son independientes cuando, 𝑃(𝐴 ∩ 𝐵)= 𝑃(𝐴) 𝑃(𝐵).
Se dice que A1, A2,...,A3 son mutuamente independientes si se cumplen todas y cada una de las sig. condiciones
𝑃(𝐴𝑖∩𝐴𝑗) = 𝑃(𝐴𝑖)𝑃(𝐴𝑗)
𝑃(𝐴 ∩𝐴𝑗∩𝐴𝑘) = 𝑃(𝐴𝑖)𝑃(𝐴𝑗)𝑃(𝐴𝑘)
𝑃(𝐴𝑖∩𝐴2∩⋯∩𝐴𝑛) = 𝑃(𝐴1)𝑃(𝐴2)…𝑃(𝐴𝑛)
