PROBABILIDAD/VARIABLE

Una variable refiere, en una primer instancia, a cosas que son susceptibles de ser modificadas (de variar), de cambiar en función de algún motivo determinado o indeterminado.
las variables pueden clasificarse en dos categorías:

Cualitativas: se dice que una variable es cualitativa cuando expresa un carácter de forma no numérica. Ejemplos: sexo (varón o hembra); color de os ojos (azul, negro, marrón ...).
Nominal: es lo que entendemos exactamente por cualitativas.
Ordinal: no se exige que la expresión del carácter sea numérica, pero s al menos que exista un orden natural establecido. Ejemplo: grado de satisfacción en una encuesta (muy bajo, bajo, medio, alto, muy alto). Téngase en cuenta que, con frecuencia, estos resultados se asocian a números (1,2,3,4 y 5).

Cuantitativas: se dice que una variable es cuantitativa o numérica cuando expresa un carácter mediante un numero real.
En este apartado podemos distinguir a su vez dos variedades:
Discretas: aquellas que solo admiten una cantidad numerable de valores, es decir, los valores que pueden tomar pueden escribirse uno detrás de otro en una secuencia. Ejemplos: número de hijos de una familia (0,1,2...); edad en años (0,1,2...); precio en euros de un producto de venta en supermercados (0.01, 0.02, 0.03...)
Continuas: aquellas que admiten cualquier valor dentro de un intervalo por lo que sus posibles valores no pueden enumerarse. Ejemplos: peso, tiempo de vida, glucemia...
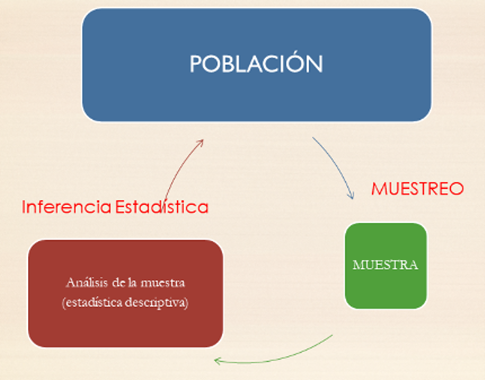
Esquema de trabajo de la estadística matemática
Subtopic
probabilidad y variable aleatoria
El objetivo de la estadística inferencial
es conocer lo mejor posible una población, a partir de una muestra de individuos. Para ello se elige una muestra de la población, lo más representativa posible de la misma, y se analiza, extrayendo toda la información que se pueda.
Función densidad de la probabilidad: Chi cuadrado
Igual que una variable aleatoria discreta viene caracterizada por su función de probabilidad, las variables aleatorias continuas vienen caracterizadas por una función llamada función de densidad, que es una generalización de la función de probabilidad.
Matemáticamente, una función es una función de densidad si verifica 𝑓dos propiedades:
es mayor o igual que cero en cualquier punto (el dibujo de 𝑓(𝑥)𝑥
la función debe estar por encima del eje horizontal)
∫∞―∞𝑓(𝑥)𝑑𝑥=1Es la media aritmética de los valores absolutos de las desviaciones con respecto a la media aritmética.
El estadístico ji-cuadrado (o chi cuadrado), que tiene distribución de probabilidad del mismo nombre, sirve para someter a prueba hipótesis referidas a distribuciones de frecuencias.

La probabilidad es: la posibilidad que existe entre varias posibilidades, que un hecho o condición se produzcan.
FORMULA
Permite medir la factibilidad de un evento. 𝑃(𝐸)=𝑁ú𝑚𝑒𝑟𝑜𝑑𝑒𝑟𝑒𝑠𝑢𝑙𝑡𝑎𝑑𝑜𝑠𝑓𝑎𝑣𝑜𝑟𝑎𝑏𝑙𝑒𝑠/𝑁ú𝑚𝑒𝑟𝑜𝑑𝑒𝑟𝑒𝑠𝑢𝑙𝑡𝑎𝑑𝑜𝑠𝑝𝑜𝑠𝑖𝑏𝑙𝑒𝑠
Cuando es imposible de que ocurra un evento, su probabilidad es 0.
Cuando se está absolutamente seguro de que el evento ocurre, su probabilidad es 1.
Fenómenos Aleatorios y Fenómenos Deterministicos

Fenómeno Aleatorio.-
Es un fenómeno del que no se sabe que es lo que va a ocurrir, están relacionados con el azar o probabilidad.
La probabilidad estudia el tipo de fenómenos aleatorios.
Experimento aleatorio.-
Una acción que se realiza con el propósito de analizarla. Tiene como fin último determinar la probabilidad de uno o de varios resultados. Se considera como aleatorio, si sus resultados no son constantes. Puede ser efectuado cualquier número de veces esencialmente en las mismas condiciones.
Un experimento es aleatorio si se verifican las siguientes condiciones
1. Se puede repetir indefinidamente, siempre en las mismas condiciones;
2. Antes de realizarlo, no se puede predecir el resultado que se va a obtener;
. El resultado que se obtenga, s, pertenece a un conjunto conocido previamente de resultados posibles.
Espacio Muestral:Es el conjunto de todos los posibles resultados de interés de un experimento dado, y se le denota normalmente mediante la letra S.undefined
Fenómeno Determinista.-
Es el fenómeno en el cual de antemano se sabe cuál será el resultado.
Tipos de eventos
Exhaustivos: Se dice que dos o más eventos son exhaustivos si se consideran todos los posibles resultados.
No exhaustivos: Se dice que dos o más eventos son no exhaustivos si no agotan todos los posibles resultados.
Mutuamente exclusivos: Eventos que no pueden ocurrir en forma simultánea.
No mutuamente exclusivos: Eventos que pueden ocurrir en forma simultánea.
Independientes: eventos cuya probabilidad no es afectada porque ocurran o no ocurran entre ellos.
Dependientes: Eventos cuya probabilidad cambia dependiendo de que ocurran o no ocurran entre si.