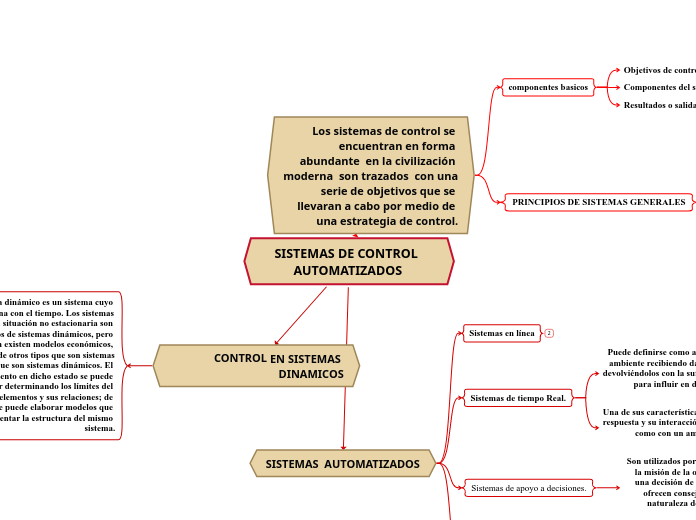
SISTEMAS DE CONTROL AUTOMATIZADOS
Los sistemas de control se encuentran en forma abundante en la civilización moderna son trazados con una serie de objetivos que se llevaran a cabo por medio de una estrategia de control.
componentes basicos
Objetivos de control
Componentes del sistema de control
Resultados o salidas
PRINCIPIOS DE SISTEMAS GENERALES
Entre más especializado sea el sistema, menos capaz es de adaptarse a circunstancias diferentes.
Cuanto mayor sea el sistema mayor es el número de sus recursos que debe dedicarse a su mantenimiento diario.
Los sistemas siempre forman parte de sistemas mayores y siempre pueden dividirse en sistemas menores.
Los sistemas crecen, no es una ley para todos pero si en la mayoría puede considerarse que no permanecerán estáticos; por lo tanto debe incluirse el costo de este crecimiento en el tiempo en los cálculos de costo - beneficio.
SISTEMAS AUTOMATIZADOS
Sistemas en línea
Sistemas de tiempo Real.
Puede definirse como aquel que controla un ambiente recibiendo datos, procesándolos y devolviéndolos con la suficiente rapidez como para influir en dicho ambiente en ese momento.
Una de sus características son la velocidad de respuesta y su interacción tanto con personas como con un ambiente generalmente autónomo y hostil.
Sistemas de apoyo a decisiones.
Son utilizados por gerentes y jefes para evaluar y analizar la misión de la organización. En lugar de consejos sobre una decisión de negocio en forma aislada, estos sistemas ofrecen consejos más amplios y generales acerca de la naturaleza del mercado, preferencia del consumidor, comportamiento de la competencia, etc.
Sistemas basados en el conocimiento.
También conocidos como sistemas expertos, son asociados al campo de la inteligencia artificial. La meta de los científicos de la computación que trabajan en este campo, es producir programas capaces de imitar el desempeño humano en una gran variedad de tareas inteligentes.
CONTROL EN SISTEMAS DINAMICOS
Un sistema dinámico es un sistema cuyo estado evoluciona con el tiempo. Los sistemas físicos en situación no estacionaria son ejemplos de sistemas dinámicos, pero también existen modelos económicos, matemáticos y de otros tipos que son sistemas abstractos que son sistemas dinámicos. El comportamiento en dicho estado se puede caracterizar determinando los límites del sistema, los elementos y sus relaciones; de esta forma se puede elaborar modelos que buscan representar la estructura del mismo sistema.