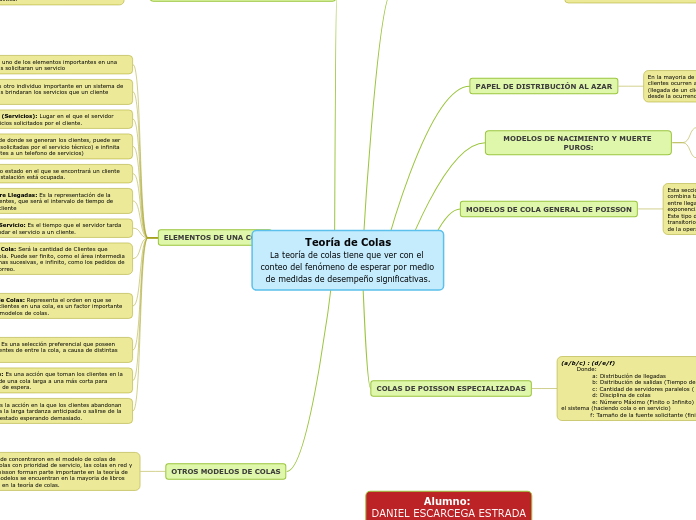
Teoría de Colas
La teoría de colas tiene que ver con el conteo del fenómeno de esperar por medio de medidas de desempeño significativas.
(M/G/1):(GD/inf/inf) -- FORMULA DE POLLACZEK - KHINTCHINE (P - K)
En esta seccion presenta una de las pocas colas no Poisson para la cual hay disponibles resultados analíticos. Este modelo no proporciona una expresión de forma cerrada debido a la incontrolabilidad analítica.
ELEMENTOS DE UNA COLA
1. Clientes: Es uno de los elementos importantes en una cola, ya que estos solicitaran un servicio
2. Servidor: Es otro individuo importante en un sistema de cola, ya que estos brindaran los servicios que un cliente solicitará.
3. Instalación (Servicios): Lugar en el que el servidor brindará los servicios solicitados por el cliente.
4. Fuente: Es de donde se generan los clientes, puede ser finita (máquinas solicitadas por el servicio técnico) e infinita (llamadas entrantes a un telefono de servicios)
5. Cola: Lugar o estado en el que se encontrará un cliente en espera si la instalación está ocupada.
6. Tiempo entre Llegadas: Es la representación de la llegada de los clientes, que será el intervalo de tiempo de llegada de cada cliente
7. Tiempo de Servicio: Es el tiempo que el servidor tarda en atender o brindar el servicio a un cliente.
8. Tamaño de Cola: Será la cantidad de Clientes que habrán en una cola. Puede ser finito, como el área intermedia entre dos máquinas sucesivas, e infinito, como los pedidos de instalación por correo.
9. Disciplina de Colas: Representa el orden en que se selecciona a los clientes en una cola, es un factor importante en el análisis de modelos de colas.
Primero en llegar, Primero en ser atendido (FCFS)
Último en llegar, Primero en ser atendido (LCFS)
Servicio de Orden Aleatorio (SIRO)
10. Prioridad: Es una selección preferencial que poseen determinados clientes de entre la cola, a causa de distintas circunstancias.
11. Cambiarse: Es una acción que toman los clientes en la que se cambian de una cola larga a una más corta para reducir el tiempo de espera.
12. Desistir: Es la acción en la que los clientes abandonan una cola debido a la larga tardanza anticipada o salirse de la cola porque han estado esperando demasiado.
OTROS MODELOS DE COLAS
Las secciones de concentraron en el modelo de colas de Poisson. Las colas con prioridad de servicio, las colas en red y las colas no Poisson forman parte importante en la teoría de colas. Estos modelos se encuentran en la mayoria de libros especializados en la teoría de colas.
MODELOS DE DECISIÓN DE COLAS
En esta sección resentaremos dos modelos de decisión que nos permitirá determinar niveles de servicio adecuado en sistemas de colas.
1. Modelo de Costos: Los modelos de costos tiene como objetivo tratar de balancear dos costos conflictivos
- El costo de ofrecimiento de servicio
- El costo de la demora al ofrecer un servicio (tiempo de espera del cliente)
Un incremento de un costo provoca automáticamente una reducción del otro. En general estos parámetros son difíciles de calcular, en particular el asociado con el tiempo de espera de los clientes.
2. Modeli de Nivel de Aspiración: El modelo de nivel de aspiración disminuye esta dificultad al trabajar directamente con medidas de desempeño de la situación de colas. La idea es determinar un intervalo aceptable para el nivel de servicio especificando límites razonables en las medidas de desempeño conflictivas (niveles de aspiración)
Se tiene en cuenta dos medidas de desempeño (conflictivas):
- El tiempo promedio en el sistema, Ws.
- Porcentaje de ociosidad de los servidores, X.
PAPEL DE DISTRIBUCIÓN AL AZAR
En la mayoria de situaciones de colas, las llegadas de los clientes ocurren a azar donde la ocurrencia de un evento (llegada de un cliente) es independiente al tiempo transcurrido desde la ocurrencia del último evento.
MODELOS DE NACIMIENTO Y MUERTE PUROS:
Modelo de Nacimiento Puro: Es un modelo en el cual solo ocurren llegadas de clientes, como la creación de actas de nacimiento de bebés recién nacidos.
2. Modelo de Muerte Pura: Es un modelo contraria a la de nacimiento puro, en el que solo ocurrirá salidas de clientes, como el retiro aleatorio de un artículo de una tienda.
MODELOS DE COLA GENERAL DE POISSON
Esta sección desarrolla un modelo de colas general que combina tanto llegadas como salidas, es decir, los tiempos entre llegadas y los tiempos de servicio siguen la distribución exponencial.
Este tipo de análisis contrasta con el comportamiento transitorio, o de calentamiento, que prevalece durante el inicio de la operacion del sistema. .
COLAS DE POISSON ESPECIALIZADAS
(a/b/c) : (d/e/f)
Donde:
a: Distribución de llegadas
b: Dsitribución de salidas (Tiempo de Servicio)
c: Cantidad de servidores paralelos ( = 1, 2, ...)
d: Disciplina de colas
e: Número Máximo (Finito o Infinito) permitidos en el sistema (haciendo cola o en servicio)
f: Tamaño de la fuente solicitante (finita o infinita)
1. Medidas de Desempeño de Estado Estable: Las medidas de desempeño mas comúnmente usadas en una situación de colas son:
Ls: Cantidad esperada de clientes en un sistema
Lq: Cantidad esperada de clientes en una cola
Ws: Tiempo de espera en el sistema
Wq: Tiempo de espera anticipado en la cola
c: Cantida esperada de servidores ocupados
Recuerde que el sistema incluye tanto la cola como las instalaciones de servicio.
2. Modelos de un solo Servidor: Esta sección presenta dos modelos para el caso de un solo servidor (c=1) . El primer modelo no limita el número máximo en el sistema , y el segundo supone un límite finito del sistema. Ambos suponen una capacidad infinita de la fuente. Las llegadas ocurren a razon de m clientes por unidad de tiempo y la tasa de servicio es u clientes por unidad de tiempo.
El resultado de ambos modelos se derivan como casos especiales de los resultados del modelo generalizado de Poisson
3. Modelos de Varios Servidores: Esta sección consideran tres modelos de colas con varios servidores paralelos. Los primeros dos usados en el Modelo de un solo Servidor y el tercer modelo trata el caso del autoservicio, el cual equivale a tener una cantidad infinita de servidores paralelos.
4. Modelo de Servicio de Máquinas (M/M/R) : (GD/K/K), R < K: La jurisdicción de este modelo es un taller con K máquinas. Cuando una máquina se descompone, se llama a uno de los técnicos en mantenimiento para que la repare. Donde la tasa de descomposturas por máquina será m por unidad de tiempo. Todas las descomposturas y servicios siguen la distribución de Poisson.
La fuente en este modelo es finita porque las máquinas que están funcionando se descomponen