Методы анализа цепей

Mai multe ca aceasta

Cloud Atlas

după Олег Красицкий

партнерская программа

după dospekhova nataliya

Групповая

după Мария Трифонова

Ремонт рекрутера Васи

după Konstantin Bagdasarov

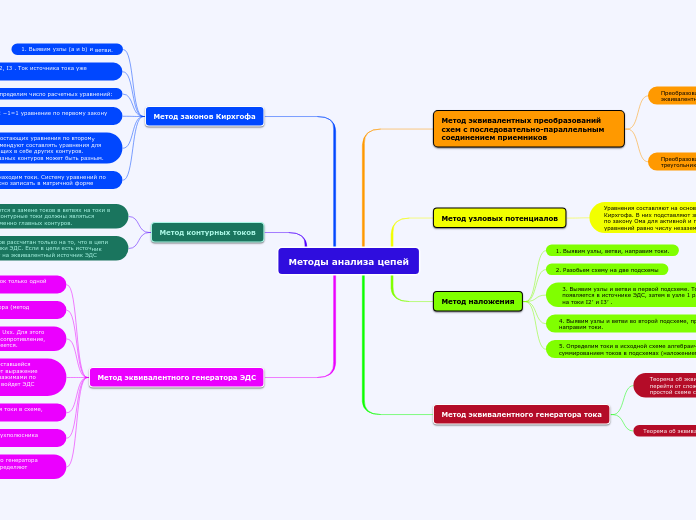
Методы анализа цепей

Conflict is present everywhere in the world around us. We experience conflict on a daily basis, and it can be minor or major.

Conflict in a story is a struggle between opposing forces. Characters must act to confront those forces and there is where conflict is born. If there is nothing to overcome, there is no story. Conflict in a story creates and drives the plot forward.

Метод эквивалентного генератора ЭДС

5. В соответствии с методом эквивалентного генератора (метод эквивалентного источника ЭДС), определяют искомый ток ветви.

4. Определяют входное сопротивление двухполюсника относительно разомкнутых зажимов.

3. Рациональным методом рассчитываются токи в схеме, вошедшие в выражение напряжения Uхх.

2. Задаются направлением токов в ветвях оставшейся схемы после размыкания ветви. Записывают выражение для напряжения Uхх между разомкнутыми зажимами по второму закону Кирхгофа. В это уравнение войдет ЭДС разомкнутой ветви.

1. Определяют напряжение холостого хода Uхх. Для этого ветвь с искомым током разрывают, удаляя сопротивление, и оставляют ЭДС в этой ветви, если она имеется.

Алгоритм метода эквивалентного генератора (метод эквивалентного источника ЭДС)

Этот метод дает возможность вычислить ток только одной ветви схемы.

Метод контурных токов

Метод контурных токов рассчитан только на то, что в цепи присутствуют источники ЭДС. Если в цепи есть источник тока, то его заменяют на эквивалентный источник ЭДС

Суть метода заключается в замене токов в ветвях на токи в контурах. Заданные контурные токи должны являться контурными токами именно главных контуров.

Метод законов Кирхгофа

6. Решением системы находим токи. Систему уравнений по законам Кирхгофа можно записать в матричной форме

5. Дописываем два недостающих уравнения по второму закону Кирхгофа. Рекомендуют составлять уравнения для «главных», не содержащих в себе других контуров. Направление обхода разных контуров может быть разным.

4. Составим (n −1) = 2 −1=1 уравнение по первому закону Кирхгофа:

3. Определим число расчетных уравнений:

2. Направим токи I1, I2, I3 . Ток источника тока уже обозначен и известен.

1. Выявим узлы (а и b) и ветви.

Метод эквивалентного генератора тока

Теорема об эквивалентном источнике тока.

Ток в произвольной ветви линейной электрической цепи не изменится, если всю внешнюю по отношению к рассматриваемой ветви цепь заменить эквивалентным источником тока, ток которого равен току короткого замыкания внешней цепи, а внутренняя проводимость – входной проводимости внешней цепи, в которой источники напряжения закорочены, а источники тока разомкнуты.

Теорема об эквивалентном источнике тока позволяет перейти от сложной схемы со многими источниками к простой схеме с одним источником тока.

Метод наложения

5. Определим токи в исходной схеме алгебраическим суммированием токов в подсхемах (наложением подсхем):

4. Выявим узлы и ветви во второй подсхеме, правильно направим токи.

3. Выявим узлы и ветви в первой подсхеме. Ток I1′ появляется в источнике ЭДС, затем в узле 1 разветвляется на токи I2′ и I3′ .

2. Разобьем схему на две подсхемы

1. Выявим узлы, ветви, направим токи.

Метод узловых потенциалов

Уравнения составляют на основании первого закона Кирхгофа. В них подставляют значения токов, выраженные по закону Ома для активной и пассивной ветвей. Число уравнений равно числу незаземленных узлов

Метод эквивалентных преобразований схем с последовательно-параллельным соединением приемников

Преобразование сопротивлений эквивалентной звезды в треугольник

Rac=Ra+Rc+RaRcRb

Rbc=Rc+Rb+RcRbRa

Rab=Ra+Rb+RaRbRc

Преобразование треугольника сопротивлений в эквивалентную звезду

Rc=RcaRbcRab+Rbc+Rca

Rb=RabRbcRab+Rbc+Rca

Ra=RabRcaRab+Rbc+Rca