Функція
Функція - одне з основних математичних і загальнонаукових понять. Воно зіграло й понині відіграє більшу роль у пізнанні реального миру.
Пропедевтичний період (з найдавніших часів до 17 століття).
Ідея функціональної залежності сходить до стародавності. Її втримування виявляється вже в перших математично виражених співвідношеннях між величинами, у перших правилах дій над числами. У перших формулах для знаходження площі й обсягу тих або інших фігур. Так, вавилонські вчені (4 - 5тис. років тому) нехай несвідомо, установили, що площа кругу є функцією від його радіуса за допомогою знаходження грубо наближеної формули: S=3r2.
Прикладами табличного завдання функції можуть служити астрономічні таблиці вавилонян, стародавніх греків і індійців, а прикладами словесного завдання функції - теорема про сталість відносини площ кругу й квадрата на його діаметрі або античні визначення конічних перетинів, причому самі ці криві виступали як геометричні образи відповідної залежності.
Квадратична функція
У математиці, квадратична функція — це поліноміальна функція з старшим членом другого порядку.
Цікавинки
У математиці, квадратична функція — це поліноміальна функція з старшим членом другого порядку.
Загальні властивості
- Область визначення квадратичної функції - вся числова пряма.
- При
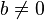 функція не є парною і не є непарною. При
функція не є парною і не є непарною. При 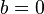 квадратична функція - парна.
квадратична функція - парна. - Квадратична функція неперервна і диференційовна на всій області визначення.
- Функція має єдину критичну точку
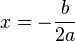 .
. - Область зміни функції: при
 - безліч значень функції
- безліч значень функції  ; при
; при  - безліч значень функції
- безліч значень функції ![(-\infty;-\frac{b^2 -4 ac}{4a}]](http://upload.wikimedia.org/math/6/f/3/6f3500e76287182968cfe33fdf9c71b9.png) .
.
y=−x2+3x−1 (показано чорним)
З малюнка видно, що вершини парабол знаходяться у різних точках. Крім того, вітки параболи, що є графіком функції y=−x2+3x−1
y=−x2+3x−1 (показано чорним), напрямлені вниз, а решти — вгору. А ще важливими є точки, у яких графік функції перетинає координатні осі.
Видатні українські математики.
Відомі українські математики
Михайло Остроградський
(1801-1862)
Георгій Феодосійович Вороний
(1868-1908)
Михайло Пилипович Кравчук
(1892-1942)
Володимир Йосипович Левицький
(1872-1956)
Мирон Онуфрійович Зарицький
(1889-1961)
Віктор Михайлович Глушков
(1932-1982)
Юрій Львович Далецький
(1926-1997)
Відео
Видатні математики України
Георгій Феодосійович Вороний народився в селі
Журавка на Полтаворонийвщині (тепер село – Варвинського району, Чернігівської області). Дослідження математика стосуються комп’ютерної графіки, аналітичної теорії чисел, геометричного моделювання, конструювання робіт, створення штучного інтелекту і застосовуються в сучасних дослідженнях. Наш співвітчизник відомий у всьому світі: у м. Сеулі (Південна Корея) діє Дослідницький центр з діаграм Вороного, а 2004 року в Токіо (Японія) були започатковані щорічні (VD) Міжнародні конференції з діаграм Вороного.
Видатний вчений мав хворобу жовчного міхура, яка принесла чимало страждань і стала причиною смерті у 1908 р.. Щоденник Георгія Вороного зберігається в Інституті Рукопису Національної бібліотеки України ім. В.І. Вернадського.
Михайло Васильович Остроградський народився 1801 р. в селі Пашенна на остроградський Полтавщині.
Роботи Михайла Васильовича присвячені теорії чисел, диференціальному та інтегральному численню, вищій алгебрі, геометрії, теорії ймовірностей, математичній фізиці, балістиці тощо. Існує метод інтегрування Остроградського, правило Остроградського, формула Остроградського…
Віктор Михайлович Глушков народився у 1923 р., дитинство його припало на воєнні роки. Пізніше майбутній учений трудився на шахті і навчався одночасно у двох внз – Новочеркаському політехнічному інституті та Ростовському університеті на механіко-математичному факультеті. Якось за десять днів сесії він склав на “відмінно” двадцять п’ять вузівських екзаменів – а ми жаліємось на 5, і не завжди блискуче їх складаємо
Його життя було нерозривним із Українською Академією Наук та Інститутом Кібернетики. Плідна праця пов’язана із теоріями цифрових автоматів, топологічних груп та топологічної алгебри, проектуванням ЕОМ (електронно-обчислювальних машин).
Авторитет В.М. Глушкова був феноменальним: у 1969 р. математик одержав понад сто запрошень, в яких йому пропонували прочитати лекції з різних питань кібернетики. Під його керівництвом створили унікальну «Енциклопедію кібернетики», а також універсальні електронно-обчислювальні машини “Київ”, “Дніпро” та інші ЕОМ. Помер вчений 30 січня 1982 р..
Вороний Г. В.
Георгій Феодосійович Вороний народився в с. Журавка на Полтаворонийвщині (тепер село – Варвинського району, Чернігівської області). Дослідження математика стосуються комп’ютерної графіки, аналітичної теорії чисел, геометричного моделювання, конструювання робіт, створення штучного інтелекту і застосовуються в сучасних дослідженнях. Наш співвітчизник відомий у всьому світі: у м. Сеулі (Південна Корея) діє Дослідницький центр з діаграм Вороного, а 2004 року в Токіо (Японія) були започатковані щорічні (VD) Міжнародні конференції з діаграм Вороного.
Видатний вчений мав хворобу жовчного міхура, яка принесла чимало страждань і стала причиною смерті у 1908 р.. Щоденник Георгія Вороного зберігається в Інституті Рукопису Національної бібліотеки України ім. В.І. Вернадського.
Глушков В. М.
Віктор Михайлович Глушков народився у 1923 р., дитинство його припало на воєнні роки. Пізніше майбутній учений трудився на шахті і навчався одночасно у двох внз – Новочеркаському політехнічному інституті та Ростовському університеті на механіко-математичному факультеті. Якось за десять днів сесії він склав на “відмінно” двадцять п’ять вузівських екзаменів – а ми жаліємось на 5, і не завжди блискуче їх складаємо
Його життя було нерозривним із Українською Академією Наук та Інститутом Кібернетики. Плідна праця пов’язана із теоріями цифрових автоматів, топологічних груп та топологічної алгебри, проектуванням ЕОМ (електронно-обчислювальних машин).
Авторитет В.М. Глушкова був феноменальним: у 1969 р. математик одержав понад сто запрошень, в яких йому пропонували прочитати лекції з різних питань кібернетики. Під його керівництвом створили унікальну «Енциклопедію кібернетики», а також універсальні електронно-обчислювальні машини “Київ”, “Дніпро” та інші ЕОМ. Помер вчений 30 січня 1982 р.
Лінійна функція
Лінійна функція задається рівнянням:
 .
.
Пояснення
Лінійна функція — це функція, яку можна задати формулою
y=kx+b, де x — незалежна змінна, k і b — деякі числа.
Властивості
Якщо k>0, тоді лінійна функція y=kx+b зростає;
якщо k<0, тоді лінійна функція y=kx+b спадає.
Означення
Графіком лінійної функції y=kx+b є пряма.
Перетворення графіків.
Для повторення шкільних матеріалів, які Ви повинні вільно вміти використовувати, уважно перегляньте таблицю в якій проілюстровані вісім основних перетворень графіка функці
Основними методами геометричних перетворень графіків функцій є симетрія відносно осей Ox, Oy;
паралельне перенесення відносно осей Ox, Oy;
стиск та розтяг графіків відносно осей; відображення частини графіка під віссю Ox нагору (аналог модуль функції) і навпаки;
поворот площини навколо певної точки. В шкільному курсі Вас навчають як геометричні перетворення використовувати до графіків функцій та як це впливає на область визначення та область значень. Всі перелічені вище перетворення необхідні, щоб швидко навчити Вас будувати графіки функцій.
Навчальний урок
Урок. Перетворення графіків функцій. (Преобразование графиков функций)
Геометричне перетворення
Основні геометричн перетворення графіка функцї
Приклад побудови
Графік перетворення функції..
Парність функції
Вивчення питання про те, чи є задана функція парною або непарною, називається дослідженням функції на парність.
Пізнавальне відео
Пояснення матеріалу про парні та непарні функції, а також їх властивості.
Парна
Функцію y=f(x), x∈X називають парною, якщо для будь-якого значення x із множини X виконується рівність f(−x)=f(x).
Непарна
Функцію y=f(x), x∈X називають непарною, якщо для будь-якого значення x із множини X виконується рівність f(−x)=−f(x).
Задання функцій
Функцію можна задавати 3 способами:
Табличний спосіб
Табличний спосіб задання функції полягає в тому, що відповідність між елементами множин 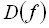 і
і 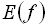 задається у формі таблиці. При цьому способі наводиться таблиця, що вказує значення функції
задається у формі таблиці. При цьому способі наводиться таблиця, що вказує значення функції 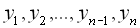 для наявних в таблиці значень аргументу
для наявних в таблиці значень аргументу 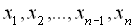
Графічний спосіб
При графічному способі задання зображають графік функції 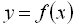 в системі координат х0у. Графіком функції називається зображення на координатній площині множини упорядкованих пар
в системі координат х0у. Графіком функції називається зображення на координатній площині множини упорядкованих пар 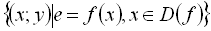 . Кожній упорядкованій парі дійсних чисел
. Кожній упорядкованій парі дійсних чисел 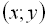 можна поставити у відповідність точку на площині. Для цього на площині зображають прямокутну (декар-тову) систему координат х0у (рис. 1). Прямі 0х і 0y взаємно перпендикулярні, 0 – точка пере-тину цих прямих. 0х – вісь абс-цис, 0y – вісь ординат, 0 – початок координат. На кожній з осей 0х і 0y вибирають позитив-ний напрям відліку (на осі 0х – зліва направо, на осі 0y – знизу угору). Вибирають також одиницю виміру (масштаб). Кожна точка
можна поставити у відповідність точку на площині. Для цього на площині зображають прямокутну (декар-тову) систему координат х0у (рис. 1). Прямі 0х і 0y взаємно перпендикулярні, 0 – точка пере-тину цих прямих. 0х – вісь абс-цис, 0y – вісь ординат, 0 – початок координат. На кожній з осей 0х і 0y вибирають позитив-ний напрям відліку (на осі 0х – зліва направо, на осі 0y – знизу угору). Вибирають також одиницю виміру (масштаб). Кожна точка 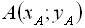 на корди-натній площині має дві коор-динати:
на корди-натній площині має дві коор-динати: 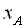 – абсцису,
– абсцису, 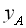 – ординату . Таким чином, графік функції
– ординату . Таким чином, графік функції 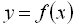 – множина точок координатної площини х0у, абсциси яких є значеннями аргументу х , а ординати – відповідні значення функції у .
– множина точок координатної площини х0у, абсциси яких є значеннями аргументу х , а ординати – відповідні значення функції у .
Аналітичний спосіб
При даному способі задання функція задається за допомогою формули 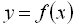 , де
, де 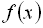 – деякий вираз із змінною х .
– деякий вираз із змінною х .


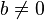 функція не є парною і не є непарною. При
функція не є парною і не є непарною. При 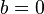 квадратична функція - парна.
квадратична функція - парна.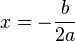 .
. - безліч значень функції
- безліч значень функції  ; при
; при  - безліч значень функції
- безліч значень функції ![(-\infty;-\frac{b^2 -4 ac}{4a}]](http://upload.wikimedia.org/math/6/f/3/6f3500e76287182968cfe33fdf9c71b9.png) .
. .
.


