realizată de Grace Smith 3 ani în urmă
180
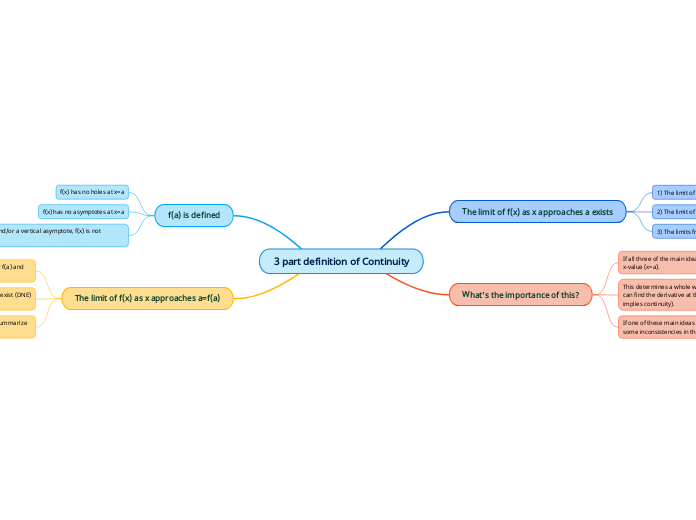
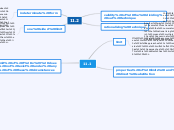
3 part definition of Continuity
A function's continuity at a specific point hinges on three key conditions. First, the function's limit must exist as it approaches the point from both the left and the right. Second, the value of the function at that point must be defined.