Albert Camus

Mai multe ca aceasta

EL AUDITOR

după ENRIQUE ALFONSO CASTILLO HERNANDEZ

Mapa conceptual (PROPORCIONALIDAD)

după Mari Caro

Husserl y la fenomenología trascendental

după carol castro

Envases y Embalajes

după Juan Jose Hernandez

Albert Camus fue un novelista, ensayista, dramaturgo, filósofo y periodista francés nacido en Argelia. Sus concepciones se formaron bajo el influjo de Schopenhauer, de Nietzsche y del existencialismo alemán.

Albert Camus

LA PESTE

BIBLIOGRAFÍAS

*https://es.wikipedia.org/wiki/Porcentaje *https://matematicascercanas.com/2015/08/25/regla-de-tres/ *https://enciclopediaeconomica.com/intervalos/ *https://es.wikipedia.org/wiki/Desigualdad_matem%C3%A1tica *https://es.wikipedia.org/wiki/Funci%C3%B3n_cuadr%C3%A1tica

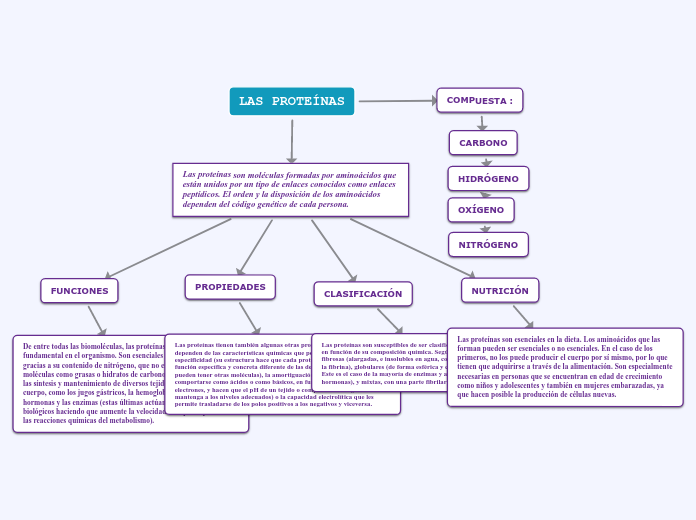
FUNCIONES CUADRÁTICAS

* Es una función polinómica con una o más variables en la que el término de grado más alto es de segundo grado. Por ejemplo, una función cuadrática en tres variables x, y, y z contiene exclusivamente los términos x2, y2, z2, xy, xz, yz, x, y, z, y una constante

Datos importantes

* La gráfica de una función cuadrática univariada es una parábola cuyo eje de simetría es paralelo al eje y, como se muestra a la derecha. * Si la función cuadrática se establece igual a cero, entonces el resultado es una ecuación cuadrática. Las soluciones a la ecuación univariable se denominan raíces de la función univariable.

FUNCIONES LINEALES

* Gráficamente en una línea recta tiene una variable independiente (ejex) - (eje y) * Todas ellas se representan mediante rectas sobre las cuales se aprecia cómo varía una magnitud respecto a la otra.

SISTEMAS DE ECUACIONES 2X2

* Se llama solución de un sistema de ecuación 2x2, a cualquier pareja de valores(x, y) que sea solución de ambas ecuaciones a la vez.

Existen diferentes métodos

* Método gráfico * Método sustitución * Método de igualación * Método de reducción

DESIGUALDADES

* Es una relación de orden que se da entre dos valores cuando éstos son distintos (en caso de ser iguales, lo que se tiene es una igualdad).

Ejemplos

• La notación a < b = a es menor que b • La notación a > b = a es mayor que b

También se puede leer como

• La notación a ≤ b a es menor o igual que b; • La notación a ≥ b significa a es mayor o igual que b;

Propiedades

Están gobernadas para las propiedades transitividad, adición, sustracción, multiplicación y división, la propiedad también se mantiene si los símbolos de desigualdad estricta (< y >) son reemplazados por sus correspondientes símbolos de desigualdad no estricta (≤ y ≥).

INTERVALOS

* Es una expresión matemática que permite incluir una infinidad de números que van de un punto a otro; el primer punto o número es el menor mientras que el segundo es el mayor.

Existen diversos intervalos

INTERVALO INFINITO: Es aquel que tiene en uno o ambos extremos un valor infinito. El extremo que posea el infinito será un extremo abierto. En caso de que ambos extremos sean infinitos, será la recta real.

INTERVALO SEMIABIERTO: Es aquel que incluye uno de los extremos, los valores que están entre ellos y el otro extremo queda excluido. Puede estar incluido o excluido el extremo derecho o izquierdo.

INTERVALO ABIERTO: Es aquel que no incluye los extremos entre los cuales está comprendido el intervalo, pero si todos los valores ubicados entre estos. Se representa mediante una expresión como a < x < b ó (a;b).

INTERVALO CERRADO: Es aquel que incluye los extremos del intervalo y todos los valores comprendidos entre ellos. Se representa con una expresión del tipo a ≤ x ≤ b ó [a;b].

INECUACIONES

* Es una desigualdad algebraica en la que sus dos miembros aparecen ligados por uno de estos signos: * f(x) < g(x), f(x) <= g(x), f(x) > g(x) o f(x)>= g(x).

* La solución de una inecuación es el conjunto de valores de la variable que verifica la inecuacíón. * Podemos expresar la solución de la inecuación mediante una representación gráfica o un intervalo

Tipos de inecuaciones

• Sistemas de inecuaciones primer° • Inecuaciones de segundo° • Inecuaciones de ° superior a dos • Inecuaciones fraccionarias • Inecuaciones con valor absoluto

REGLA DE 3

* Es una forma de resolver problemas de proporcionalidad entre tres valores conocidos y una incógnita, estableciendo una relación de proporcionalidad entre todos ellos.

Se divide en

• Regla de 3 directa (+ o -) • Regla de 3 inversa (derecho) • Regla de 3 mixta (ambas)

PORCENTAJES

* Es un símbolo matemático representado por una cantidad dada de la fracción en 100 partes iguales. * Se denota utilizando el símbolo «%», que matemáticamente equivale al factor 0,01 el cual se debe escribir después del número al que se refiere, dejando un espacio de separación.

Ejemplo

9/10 = 90 %