realizată de Victor Nunez 6 ani în urmă
513
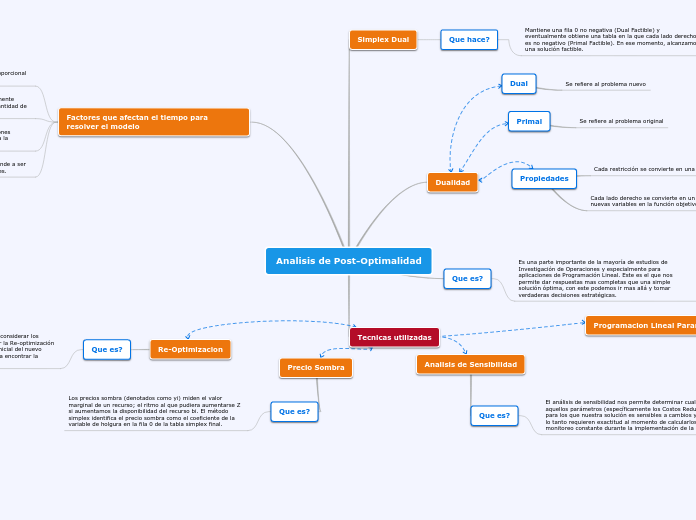
Analisis de Post-Optimalidad
En el ámbito de la optimización y la investigación operativa, existen varios conceptos clave que son fundamentales para entender y resolver problemas complejos. La re-optimización implica la creación de variantes de un modelo básico para adaptarse a diferentes escenarios, lo que permite encontrar soluciones óptimas con pocas iteraciones adicionales.