realizată de Robert Trujillo 3 ani în urmă
148
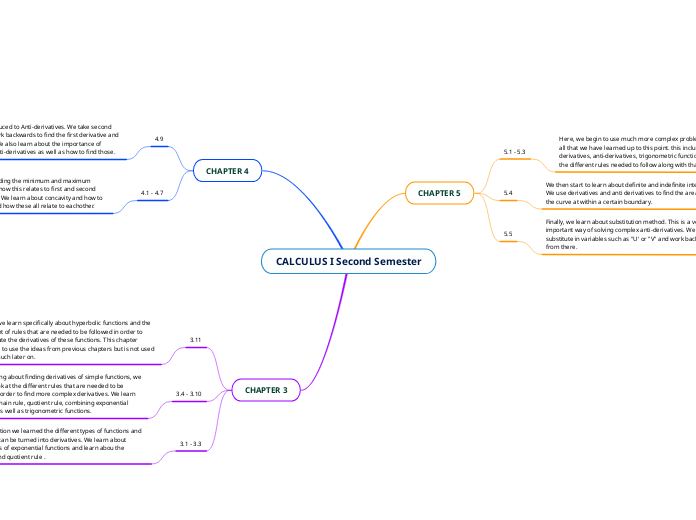
CALCULUS I Second Semester
In the second semester of Calculus I, students progress from basic derivative concepts to more advanced techniques and applications. Initially, the focus is on transforming various types of functions into their derivatives, with an emphasis on exponential functions and the introduction of the product and quotient rules.