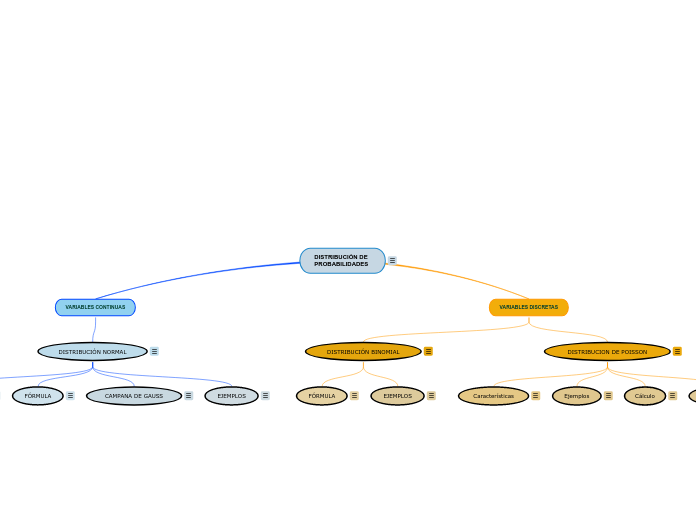
DISTRIBUCIÓN DE PROBABILIDADES
La distribución de probabilidad, se refiere a todos los resultados posibles que pueda tener una variable aleatoria, es decir, describe el comportamiento de dicha variable dentro de un intervalo de valores o de posibles resultados.
VARIABLES DISCRETAS
DISTRIBUCION DE POISSON
Fue desarrollada por Siméon Denis Poisson, este tipo de distribución, explica la probabilidad de que cierto evento ocurra un determinado número de veces en un tiempo establecido
Aplicaciones
Sus principales aplicaciones hacen referencia a la modelización de situaciones en las que nos interesa determinar el número de hechos de cierto tipo que se pueden producir en un intervalo de tiempo o de espacio o de área, bajo supuestos de aleatoriedad y ciertas circunstancias restrictivas
Cálculo
La distribución de Poisson, se refiere a ciertos procesos que pueden ser descritos con una variable aleatoria discreta. La letra X suele representar esa variable y puede además asumir valores enteros (0,1,2,3 etc..) Se utiliza la letra X mayúscula para representar la variable aleatoria y la x minúscula para designar un valor específico que puede asumir la X mayúscula. La probabilidad de exactamente x ocurrencias en una distribución de Poisson se calcula mediante la fórmula
P(x) = l x * e-l / x!
Ejemplos
- Número de aviones que aterrizan en un aeropuerto por día, hora, minuto, etc.
- Número de bacterias por cm 2 de cultivo
- Número de llamadas telefónicas a un conmutador por hora, minuto, etc.
- Número de llegadas de embarcaciones a un puerto por día, mes, etc
Características
La distribución de Poisson es una distribución de probabilidad discreta y se emplea para describir procesos que pueden ser descritos con una variable aleatoria discreta. ... Pueden ser descritos por una variable aleatoria discreta que asume valores enteros (0,1,2,3,4,5 y así sucesivamente).
DISTRIBUCIÓN BINOMIAL
Fue desarrollada por Jacob Bernoulli, posee diversas aplicaciones en el área de bioestadística, específicamente en la realización de experimentos, también es conocida como distribución de Bernoulli.
Un experimento o estudio tiene una distribución binomial cuando se cumplen las siguientes condiciones:
· En el experimento solo existen dos posibles resultados, el éxito o el fracaso.
- La repetición del mismo experimento presenta un resultado que es independiente de los resultados anteriores.
- La probabilidad del éxito o del fracaso es constante.
- Cada experimento posee un mismo número de réplicas.
Se aplica a experimentos y relaciones en las áreas de medicina o biología, aunque también puede ser aplicada en las finanzas y economía. Algunos ejemplos de su aplicación son:
· Si una persona presenta o no una enfermedad como cáncer, viruela, o hepatitis.
· Si una mujer se encuentra o no embarazada.
· Si la publicación de un artículo fue exitosa o no.
Probabilidad de r éxitos en n ensayos es :
N! / R! (N-R)! PR QN-R
VARIABLES CONTINUAS
DISTRIBUCIÓN NORMAL
La distribución normal es un modelo teórico capaz de aproximar satisfactoriamente el valor de una variable aleatoria a una situación ideal. En otras palabras, la distribución normal adapta una variable aleatoria a una función que depende de la media y la desviación típica.
EJEMPLOS
- El efecto de un medicamento o fármaco.
- El cambio de temperatura en una época del año específica.
- Caracteres morfológicos como el peso o la estatura en un grupo de individuos.
CAMPANA DE GAUSS
Esta distribución considera dos parámetros, los cuales son el promedio o la media (μ) y la desviación estándar (σ). Gracias a estos dos parámetros, tiene asociada una ecuación, de la cual se desarrolla una gráfica conocida como campana de Gauss.
FÓRMULA
z = (x – μ) / σ sigue la distribución normal estándar N(z; 0,1). El cambio de la variable x a la z recibe el nombre de estandarización o tipificación y es de gran utilidad a al momento de aplicar las tablas de la distribución estándar a los datos que siguen una distribución normal no-estándar
IMPORTANCIA
Es una de las más importantes en el área de estadística. Su desarrollo y explicación se les atribuyen a diferentes investigadores, especialmente a Carl Friedrich Gauss.
IMPORTANCIA
Muchas variables continuas comunes en el mundo de los negocios tienen distribuciones que se asemejan estrechamente a la distribución normal.
La distribución normal sirve para acercarse a diversas distribuciones de probabilidad discreta, como la distribución binomial y la distribución de Poisson.
La distribución normal proporciona la base para la estadística inferencial clásica por su relación con el teorema de límite central.