realizată de William Lozano 3 ani în urmă
343
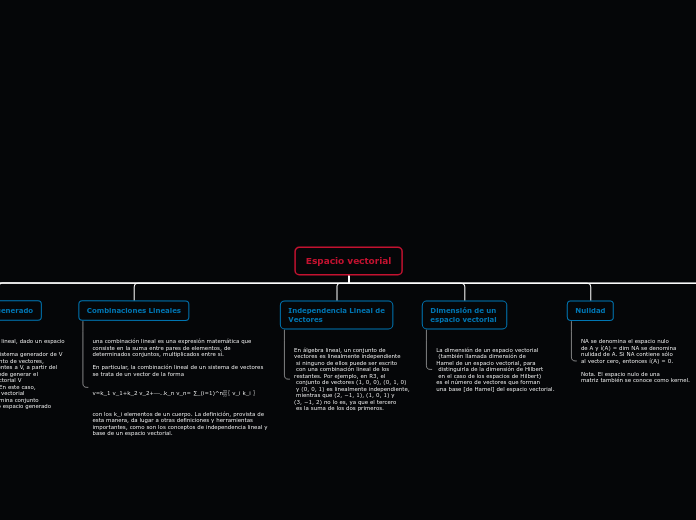
Espacio vectorial
En álgebra lineal, la independencia lineal de vectores se refiere a que ningún vector en un conjunto puede ser expresado como una combinación lineal de los demás. Esto se ejemplifica con vectores en R3, donde algunos conjuntos son independientes y otros no.