realizată de Domencia Lincango 2 ani în urmă
726
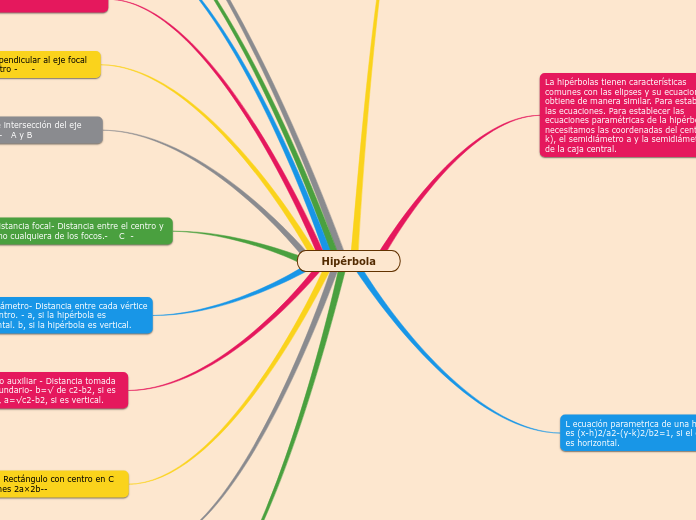
Hipérbola
Una hipérbola es un lugar geométrico definido por la diferencia constante entre las distancias a dos puntos fijos denominados focos. Los vértices son los puntos de intersección del eje focal con la hipérbola, mientras que el eje focal es la línea que pasa por ambos focos.