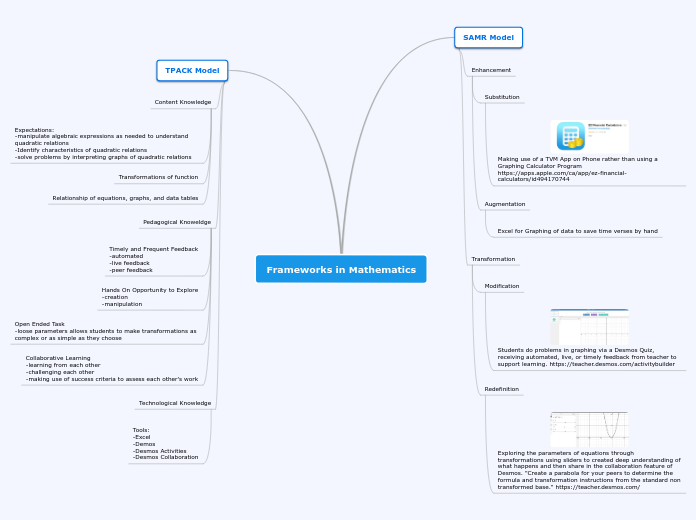
Kelley Cannady Elementary Mathematics
Integers Decimals and Percents
Adding, Subtracting, Multiplying, Dividing Decimals
Adding- When adding decimals the decimals should line up
Subtracting- Same rule as adding
Multiplying- When multiplying decimals need not line up but the final product should have the decimal moved the amount of spaces of both decimals added up
Dividing- when dividing, the decimal that is the divisor should have the decimal moved to the end. The dividend should then be given as many 0s to the end of the number that is equal to the number of decimal places moved.
Repeating Decimals
Repeating Decimals-will have a bar over the repeating digits and go on infinitely. Repeating digits are not very accurate so it is best to leave it in fraction form if at all possible. For example 1/3 in decimal for is .333......
Percents and interest
Percent=per 100
Percentage can be found by dividing the numerator by the denominator
for example to find the percentage of 4/5 you would divide 5 into four and get .8 since percentages are not decimals, we would move the decimal twice to the right and get 80%
There are many real life applications for percentage such as taxes and sales.
Introducing to finite decimals
Finite Decimals- Are decimals that have a definite end. Examples of finite decimals include decimals such as .12433456 or .12
Theorem- fraction a/b can be written as a terminating decimal if, and only if, the prime factorization of the denominator contains no primes other than 2 or 5
Probability
Permutations and Combinations
Permutation: nPr= n!/(n-r)!
This equation is used in a situation where order matters such as when choosing who wins 1st, 2nd, or 3rd place. The variable n is the total number of options available and the variable r is the number of things you're going to pick. The ! means that the number will be multiplied in descending order such as 4! is multiplied as 4*3*2*1
Combination nCr= n!/r! (n-r)!
The equation for combinations is when order does not matter such as when you are see how many different ways you can organize a group. The variable n is the total number of options available and the variable r is the number of things you're going to pick. The ! means that the number will be multiplied in descending order such as 4! is multiplied as 4*3*2*1
Determining Probabilities
Definition of Probability: P(A)= NumberofelementsofA/NumberofelementsofS
Or in other words; Number of times the event is likely to occur/Number of trials
Rational Numbers and Proportional Reasoning
Multiplication, Division, and Estimation with Rational Numbers
When Multiplying fractions you multiply the top by the top (multiply numerators together) and the bottom by the bottom (multiply denominators together) For example: 4/5*1/4= 4/20
but the fraction must be simplified and it can be reduced to 1/5
Dividing fractions is done by flipping the second number and multiplying it to the other fraction, for example: 4/5*2/7= 4/5*7/2=28/10 and can be reduced to 14/5
Addition, Subtraction, and Estimation with Rational Numbers
In the addition and subtraction of fractions, the denominator must be the same. Example: 1/3+1/9= 3/9+1/9=4/9
Number Theory
GCD and LCM
Greatest Common Divisor:
Definition: The largest positive integer that divides each of the integers.
Can be found using intersects model and prime factorization
Least Common Multiple:
Definition: The smallest number they can both divide equally into.
Can also be found using intersects model and prime factorization
Prime and Composite Numbers
Prime and Composite Numbers:
Prime Number Definition: Can only be divided into equally by itself and 1. Ex: 3,5,7,11,13,etc.
Composite Number Definition: A whole number that can be divided equally by more numbers than itself and 1.
Divisibility
Divisibility:
Definition: A set of rules that can quickly determine if one whole number is divisible by another.
How To Tell If A Number is Divisible By:
2: The last digit in a number is divisible by 2 ex:174
3: The sum of the digits is divisible by 3 ex: 732
4: The last two digits in a number is divisible by 4 ex: 220
5: The last digit is a 5 or a 0 ex: 210
6: The number is divisible by both 2 and 3 ex: 732
8: The last three digits are divisible by 8
9: The sum of the digits is divisible by 9
10: The last digit is 0
Number System and Whole Number Operations
Definition of Whole Number
Examples of Whole Number:
{0,1,2,3,4,5,6,7,8.....}
Cannot be a decimal, cannot be negative
Other Words to Know:
Cardinal Number: A number representing a quantity
Binary Operations: addition, subtraction, multiplication, and division
Disjoint: Having nothing in common
Finite: a defined amount
Set: A group of numbers
...: "and the pattern continues"
>,<: greater than, less than
Basic addition facts: Those involving a single digit and a single digit
Multiplication and Division
Division:
Dividend: A number that is divided by another
Divisor: A number dividing another number
Quotient: The answer in a division problem
Inverse: Reversed
Partition: Dividing
Multiplication:
Factors: What's being multiplied together
Product: The answer in a multiplication problem
Multiplication has the same properties as addition. These properties do not work for subtraction and division.
Strategies for Modeling the Multiplication of Whole Numbers:
Repeated-Addition Model: 4x3=4+4+4=12
Array and Area Model: Draw a grid and count the points of intersection. Can be used for tiles and other area models.
Cartesian Product Model: Create a Tree. Can be used for situations like how many outfits someone can wear.
Whole Number Multiplication Properties:
Closure Property: If a and b are whole numbers then axb is a whole unique number
Commutative Property: axb=bxa
Associative Property: (axb)xc=ax(cxb)
Distributive Property: 5x(3+4)=5x7=5x3+5x4
Addition and Subtraction
Strategies for the addition of whole numbers include:
Counting On: Counting one by one, starting from the larger number, until you reach your answer
Set Model: Modeling disjoint numbers and combining them
Number Line Model: A strategy that visually draws it out and counts it on.
Others to know: Doubles, Making 10, Counting Back
Whole Number Addition Properties:
Closure Property: The sum of two whole numbers exist and is a unique whole number
Commutative Property: "order property" a+b=b+a
Associative Property: (a+b)+c=a+(b+c)
Identity Property: a+0=a
Strategies for the Subtraction of Whole Numbers Include:
Take Away Model: A visual way to see objects being taken away
Missing Addend: a-b=____ can be found by b+___=a
Comparison Model and Number Line Model are also included
First number must be bigger otherwise it will not equal a whole number.