realizată de LEONARDO CHEPPER PUMACAHUA APAZA 2 ani în urmă
191
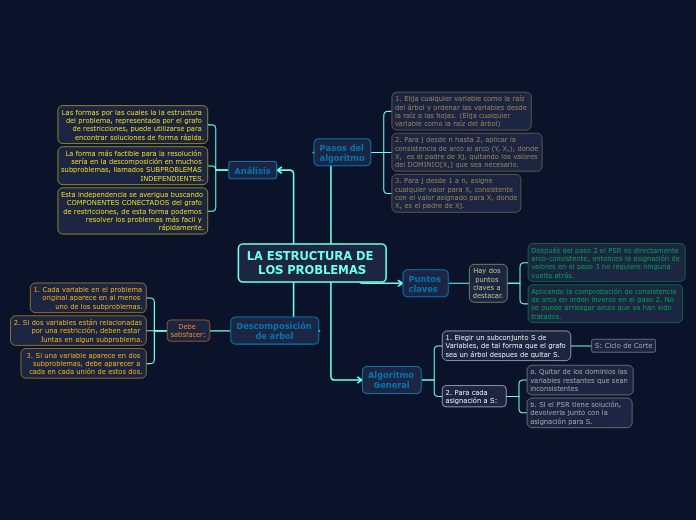
LA ESTRUCTURA DE LOS PROBLEMAS
La estructura de los problemas de restricción se aborda resaltando la importancia de la consistencia de arco y la descomposición en subproblemas. Se establece que, una vez verificada la consistencia de arco, la asignación de valores se puede hacer sin necesidad de retroceder.