Estadística descriptiva y probabilidad: teoría y problemas
medidad de dispersion
Recorrido intercuartılico
El recorrido y el rango
Varianza y desviacion tıpica
desviacion absoluta
Por los procesos de recogida de datos, censos y registros sistematicos, asumiendo un papel similar a una aritmetica estatal
Variables y atributos
las observaciones resultantes del experimento sean de tipo cualitativo o cuantitativo, en el primero de los casos se tiene un atributo y en el segundo una variable
Clasifica en series estadisticas
dependencia temporal
Temporales. Los valores se toman en instantes o perıodos de tiempo.
Atemporales. No dependen de ningun soporte temporal.
su dimension
Unidimensionales
Bidimensionales
n-dimensionales
su obtencion
objetivas:metodos exactos de medicion.
subjetivas:Obtenidas mediante apreciaciones personales.
su numero
infinita:numero finito de elementos
finita:infinitos elementos.
Momentos de la distribucion
visiones parciales de la distribucion, se pretende dar ahora una herramienta eficaz que generalice esa idea
transformaciones
hacer mas regular la distribucion y, por tanto, con mejores condiciones para su estudio.
Medidas centrales
una serie de medidas que resuman toda esa informacion y que, “de alguna manera”, representen a la distribucion.
medidas
1.Para su obtencion deben utilizarse todas las observaciones.
2. Debe ser un valor comprendido entre el menor y el mayor de los valores de la distribucion.
3. Debe venir expresada en la misma unidad que los datos.
la mediana
el que deja la mitad de las observaciones en la recta real a la izquierda y la otra mitad a la derecha
la moda
es el valor que mas veces se repite
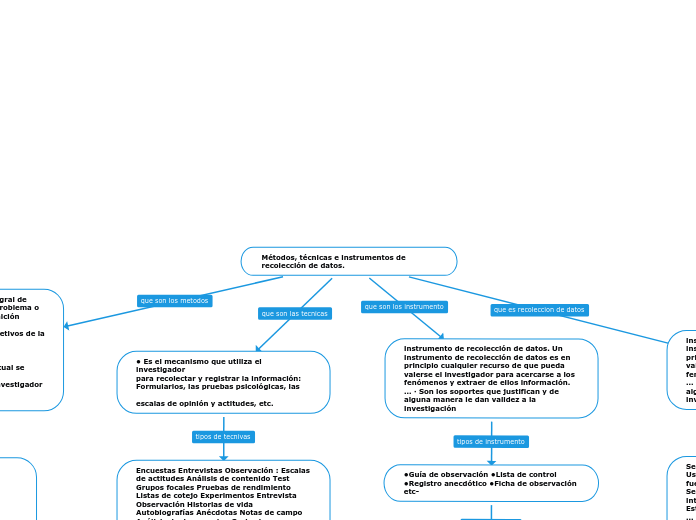
organiza la informacion
establecer distintas clasificaciones
pruebas, experimentos, valoraciones, mediciones, observaciones
Distribucion de datos
facilita los calculos posteriores y evita posibles confusiones.
Variables discretas y continuas
representaciones graficas
la naturaleza de los datos y de la forma en que estos se presenten existen distintos tipos
Un diagrama de puntos.
un diagrama de barras
El diagrama de tarta se emplea para representar atributo
histograma
que es continua cuando puede tomar cualquier valor dentro de un intervalo.
variable es discreta cuando entre dos valores consecutivos no toma valores intermedios
unión
de dos sucesos es el subconjunto de elementos del espacio muestral que están incluidos en al menos uno de esos sucesos.
intersección
de dos sucesos es el subconjunto de elementos del espacio muestral que, simultáneamente, están incluidos en los subconjuntos de ambos sucesos.
complementario
de un suceso es el subconjunto de sucesos elementales el espacio muestral que no forman parte de ese suceso.
suceso
es cualquier subconjunto de los elementos de un espacio muestral.
excluyentes
incompatibles
verifi cación
de un suceso elemental es la observación de ese suceso elemental al realizar el experimento aleatorio.
suceso elemental
es cada uno de los resultados posibles de un experimento aleatorio, su conjunto constituye el espacio muestral (E) del experimento aleatorio.
experimento aleatorio
es toda acción cuyo resultado no se puede predecir con certeza
Introducción a la probabilidad
DEFINICIÓN DE PROBABILIDAD
La probabilidad de un suceso, A, dada la verifi cación de otro suceso, B, se llama probabilidad condicional de A dado B, y es igual a la probabilidad de su intersección dividida por la probabilidad de la condición.
P(A | B) =P(A ∩ B)/P(B)
Enfoque clásico o a priori
Si la probabilidad de un suceso A es P(A) y se realizan N ensayos, inde- pendientemente y bajo las mismas condiciones, entonces la probabilidad de que la frecuencia relativa de aparición de A difi era de P(A) en una cantidad arbitrariamente pequeña, ε (siendo ε > 0), se acerca a cero a medida que crece el número de ensayos.
P (� nA/N− P(A) � ≥ ε) → 0 Si N → ∞
Probabilidad
La probabilidad de un suceso es un número que cuantifi ca en términos relativos las opciones de verifi cación de ese suceso.
Enfoque frecuencialista o a posteriori
Desde el enfoque clásico o a priori, que exige asumir el principio de indife- rencia, se defi ne la probabilidad de un suceso como la frecuencia relativa de ese suceso en el espacio muestral.
P(B) = nB/N = 6/10 = 0,60
Probabilidad de un suceso = Número de casos favorables/ Número de casos posibles
De la forma de defi nir la probabilidad desde este enfoque se deducen algunas consecuencias y propiedades:
y como consecuencia
P(A′) = 1 − P(A)
La suma de las probabilidades de un suceso y su complementario es igual a 1. Es decir:
P(A) + P(A′) = nA/N+ nA′ N= nA/N+ N −nA/N= nA − nA + N/N= 1
Un suceso que contiene todos los sucesos elementales del espacio muestral (nA = N) tiene una probabilidad igual a 1; por ello recibe el nombre de suceso seguro. Si A es un suceso seguro, entonces:
P(A) = nA/N= N/N = 1
Un suceso que no contiene ningún suceso elemental tiene una probabili- dad igual a 0; por ello recibe el nombre de suceso imposible. Si A es un suceso de este tipo, entonces:
P(A) = 0/N= 0
La probabilidad de un suceso es un valor comprendido entre 0 y 1:
0 ≤ P(A) ≤ 1
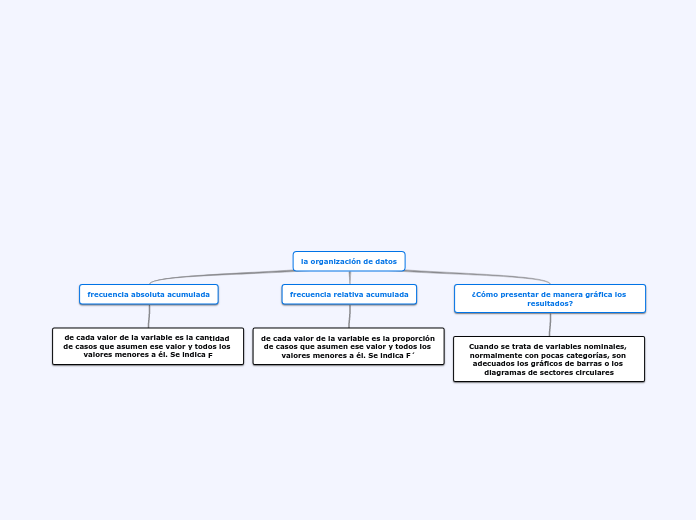
la organización de datos
¿Cómo presentar de manera gráfica los resultados?
Cuando se trata de variables nominales, normalmente con pocas categorías, son adecuados los gráficos de barras o los diagramas de sectores circulares
frecuencia relativa acumulada
de cada valor de la variable es la proporción de casos que asumen ese valor y todos los valores menores a él. Se indica F´
frecuencia absoluta acumulada
de cada valor de la variable es la cantidad de casos que asumen ese valor y todos los valores menores a él. Se indica F