Measurement

Mai multe ca aceasta

Basic Measurement for Elementary Students

după Jackie Lindquist

Measurement & Trigonometry

după Vita Gamito

Measurements

după Shania Holst

Geometry K-6

după Dana Merkel

Converse of the Pythagorean Theorem

Let a triangle have sides of length a, b, and c. If a^2 + b^2= c^2, then the triangle is a right triangle and the angle opposite the side of length c is the right angle.

The Addition Property of Area

If a region R is dissected into nonoverlapping subregions A, B, ..., F, then the area of R is the sum of the areas of the subregions:

area(R)= area(A) + area(B) + ... + area(F)

The Congruence Property of Area

If region R is congruent to region S, then the two regions have the same area:

area(R)=area(S)

Congruence of Two Regions in the Plan

If R and S are regions in the plane that have the same size and shape, then they are CONGRUENT and we use the ≅ symbol to write R≅S.

Practice Games!

Formulas & Examples

Practice Problems!

Measurement: Length, Area, & Volume

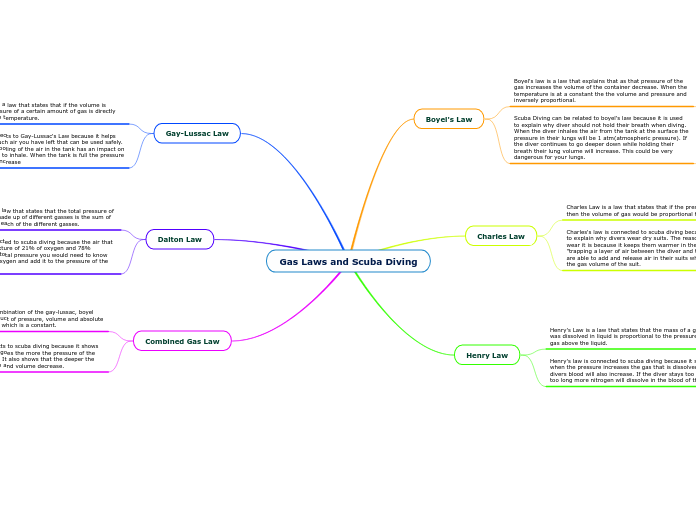
Surface Area

Surface Area of a Sphere

$S= 4(pi)r^2$

r represents radius, which is half of the diameter

Surface Area of a Right Circular Cone

$SA= (pi)r^2 + (pi)rs$

s represents the slant height

r represents the radius, which is half of the diameter

Surface Area of a Right Regular Pyramid

$SA= B + 1/2ps$

s represents the slant height, since triangles do not have a line straight up and down.

p represents the perimeter of the triangle

Surface Area of a Right Prism or Right Cylinder

$SA= 2B + ph$

h represents the height of the prism or cylinder

p represents the perimeter of each base

Volume

Volume is the amount of space that is enclosed inside a boundry. Finding this is important and useful if you want to find how much of something can be held within a boundry.

Volume of a Sphere

The volume of a sphere formula is:

V= 4/3(pi)r^3

This formula is usually the most confusing one to do. On your calculator you can use either the pi symbol or you can multiply it by 3.14. The "r" stand for radius, which is half of the diameter.

Volume of a Pyramid or a Cone

The volume of a pyramid or a cone formula is:

V= 1/3Bh

Volume of a General Prism

The the volume of a general prism formula is:

V=Bh

Volume of a Right Prism or a Right Cylinder

The volume of a right prism or a right cylinder formula is:

V= Bh

The B= to the area of the base

Volume of a Rectangular Box

The volume of a rectangular box has the formula of:

V=lwh

Area and Perimeter

Perimeter

If a region is bounded by a simple closed curve, then the PERIMETER of the region is the length of the curve. More generally, the PERIMETER of a region is the length of its boundry.

The Circumference of a Circle

Area

Let R be a region and assume that a unit of area is chosen. The number of units required to cover a region in the plane without overlap is the AREA of the region R.

Area of a Circle

Area of a Trapezoid

Area of a Triangle

Area of a Parallelogram

Area of a Rectangle

The Pythagorean Theorem

The sum of the area of the squares on the legs of a right triangle is equal to the area of the square on the hypotenuse.

The Measurement Process

The measurement process is an essential process in knowing the size of something. This process has a very long history in comparing what you have to a special size. Measurements have long been practices by comparing items to parts of your body.

Metric Units: The International System

The metric system of measurement originated in France around 1789. In many efforts to get the U.S. to use the system they failed (That is why we have our own system of measurements), but Great Britain, Canada, Australia, and New Zealand did adopt this system. There is a huge advantage to using the Metric System, as it is easy to campare due to the use of the powers of ten. Instead of going from inches to feet by adding a bunch of numbers, you move a decimal.

EX:

1234 km to 1.234 m

Metric Units of Length

The SI Decimal Prefixes

Kilo (10^3)

Hecto (10^2)

Deka/Deca (10^1)

Basic unit (10^0)

Deci (10^-1)

Centi (10^-2)

Milli (10^-3)

Micro (10^-6)

The U.S. System of Measures

Units of Capacity

Teaspoon

Tablespoon

Fluid Ounce

Cup

Quart

Gallon

Units of Volume

Cubic Inch

Cubic Foot

Cubic Yard

Units of Area

Square Inch

Square Foot

Square Yard

Acre

Square Mile

Units of Length

Inch

Foot

Yard

Rod

Furlong ("furrow long" has to do with Agriculture)

Mile

Subtopic

Starting the Process

(i) Choose the property, or attribute (such as length, area, volume, capacity, temerature, time, or weight), of an object or even that is to be measured.

(ii) Select an appropriate unit of measurement.

(iii) Use a measurement device to "cover", "fill", "time", or otherwise provide a comparison of the object with the unit.

(iv) Express the measurement as the number of units used.