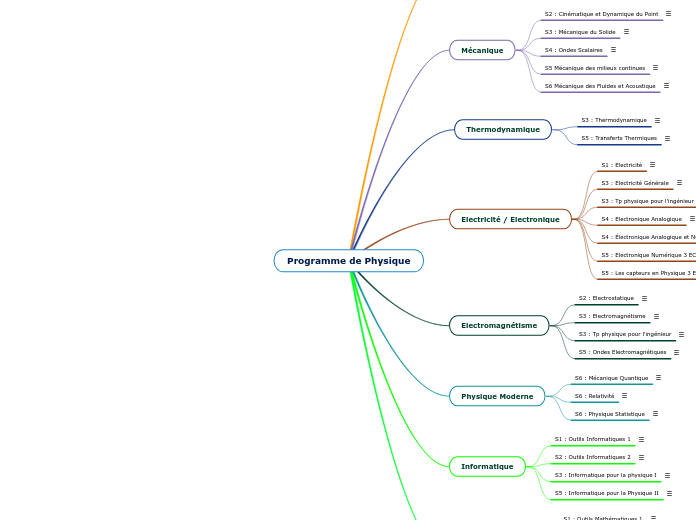
Programme de Physique
Mathématiques
S5 : Modélisation Mathématique pour la Physique et la Mécanique
UE Modélisation Mathématique pour la physique et la mécanique (20h CM, 30h TD)
Responsable de l’enseignement
Colombier Jean-Philippe jean.philippe.colombier@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
1. Vecteurs et tenseurs dans un espace Cartésien : Espaces vectorielles, Transformations orthogonales,
Dérivation des vecteurs, Produits des vecteurs, L’angle solide et la loi de Gauss, Tenseurs
2. Les champs vectoriels : Les champs gravitationnel et électrostatique, Le gradient d’une fonction scalaire, Le gradient et la dérivée directionnelle, La divergence d’un champ vectoriel, Conductivité thermique et la diffusion, L’intégrale curviligne, Circulation et le rotationnel, Les identités différentielles et intégrales vectorielles, Magnétostatiques
3. Coordonnées curvilignes : Coordonnées Cartésiennes, cylindriques et sphériques, Transfomations de coordonnées admissibles et jacobiens, Vecteurs de base et de la base réciproque, L’opérateur gradient, La vitesse et l’accélération, Divergence, rotationnel et laplacien
4. Les équations aux dérivées partielles : La méthode des caractéristiques, Les équations linéaires de l’ordre second, Séparation des variables, Solutions en séries des équations différentielles ordinaires
5. Les équations aux dérivées partielles dans la physique : La conductivité thermique et la diffusion, L’équation de Schroedinger, Ondes élastiques, Hydrodynamique et Aérodynamique, Ondes électromagnétiques
6. Séparation des variables : La méthode de transformée Fourier, Le théorème de Sturm-Liouville, Coordonnées cylindriques, Coordonnées sphériques
7. Fonctions spéciales : Fonctions de Bessel, Fonctions de Bessel de l’ordre demi-entier, Zéros d’une fonction de Bessel, La transformée de Fourier-Bessel, Polynômes de Legendre, Fonctions de Legendre associées
Prérequis :
S4 : Outils Mathématiques 4
UE Outils Mathématiques (20 CM, 20 TD)
Responsable de l’enseignement
Objectifs pédagogiques :
Syllabus :
Prérequis :
S3 : Outils Mathématiques 3
UE Outils Mathématiques III (20h CM, 30h TD)
Responsable de l’enseignement
Fedrico Pellarin : Federico.Pellarin@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
· Fonctions de plusieurs variables / Intégrales multiples
· Séries et intégrales généralisées
· Séries de Fourier
Prérequis :
UE Outils Mathématiques II (UE S2MIPC21)
S2 : Outils Mathématiques 2
UE Outils Mathématiques II (20h CM, 30h TD)
Responsable de l’enseignement
Objectifs pédagogiques :
Syllabus :
Primitives et Equations différentielles
- Calcule de primitive
- Equation linéaire du premier ordre ( , cas particulier ou ; équation homogène, méthode de variation de la constante)
- Equation différentielle du second ordre , et scalaire, application continue à valeur dans . cas particulier ou
Suite
- Généralité sur les suites réelles (def, suites arithmétiques, géométriques…)
- Limite d’une suite réelle
Développement limité
- Développement en série de Taylor au voisinage de 0
- Développement limité usuel ( , , , …)
- Introduction aux espaces Vectoriels
Prérequis :
S1 : Outils Mathématiques 1
UE Outils Mathématiques (20h CM, 30h TD)
Responsable de l’enseignement
Objectifs pédagogiques :
Syllabus :
Etude de fonctions :
- Ensemble de définition
- Limites , croissances comparées de terminales
- Dérivée
- Tableau de variation
- Recherche d’asymptotes oblique, horizontales, verticales
- Points d’inflexion
- Fonctions convexes : donner la définition et le th dans le cas f dérivable, à dérivée croissante implique f convexe (pas de démonstration)
Exemples :
- Fonctions trigonométriques : sinus, cosinus, tangente, cotangente
- Fonction exponentielle, fonction ln, ch, sh, th
Calcul d’aires avec les primitives
Nombres complexes
- Révisions du cours de Terminale S
Fonction :
- Limite d’une fonction avec epsilon
- Opérations algébriques sur les limites, démonstration des résultats
- Critères de comparaison pour les limites d’une fonction et démonstration
- Continuité, dérivabilité (juste les définitions avec la limite) et des exemples de calculs (retrouver la dérivée de x -> x^2, ….)
Prérequis :
Informatique
S5 : Informatique pour la Physique II
UE Informatique pour la physique et la vision (12 h CM,18h TD)
Responsable de l’enseignement
Marin Emmanuel emmanuel.marin@univ-st-etienne.fr
Colombier Jean-Philippe jean.philippe.colombier@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
1-Rappel sur l’architecture des ordinateurs
2-Généralités sur le langage C
3-Constantes, variables et types de base
4-Les expressions C
5-Les structures de contrôle
6-Les pointeurs
7-Les fonctions
8-Les types dérivés
9-Structures de données
(18 h de TD sur machine )
C : Premiers Pas, Tableaux, Pointeurs -Tableaux bidimensionnels - Allocation dynamique, Image - Structures – Flux
Prérequis :
S3 : Informatique pour la physique I
UE Informatique Pour la physique (16h CM, 16h TD, 18 TP)
Responsable de l’enseignement
Rémi Emonet : Remi.Emonet@univ-st-etienne.fr
Objectifs pédagogiques :
• Expliquer les bases de la programmation impérative en Python.
• Utiliser de façon approfondie de la ligne de commande (bash).
• Utiliser efficacement les bibliothèques scientifiques de Python.
• Comprendre les limitations du calcul en virgule flottante.
• Apprendre à structurer et tester un programme.
• Ecrire des programmes simples de simulation numérique.
Syllabus :
Prérequis :
S2 : Outils Informatiques 2
S1 : Outils Informatiques 1
UE Outils Informatiques (??)
Responsable de l’enseignement
Objectifs pédagogiques :
Syllabus :
Prérequis :
Physique Moderne
S6 : Physique Statistique
UE Physique statistique (10h CM, 15h TD, 6h TP)
Responsable de l’enseignement
Boukenter Aziz aziz.boukenter@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
1-Hypothèses et définitions fondamentales – Postulat d’évolution
2-Le système à N particules
3-Retour sur le gaz parfait quantique
4-La loi de Boltzmann et la statistique de Maxwell-Boltzmann
5-La statistique de Bose-Einstein
6-La statistique de Fermi-Dirac
Prérequis :
S6 : Relativité
UE Relativité (10h CM, 15h TD, 6h TP)
Responsable de l’enseignement
Colombier Jean-Philippe jean.philippe.colombier@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
1-Les limites de la mécanique classique : Expérience de Michelson Morley
2-La transformation de Lorentz : Postulats de la mécanique relativiste, La Transformation de Lorentz
3-Les conséquences de la transformation de Lorentz : Dilatation du temps, Contraction des longueurs, Principe de causalité
4-Dynamique relativiste : Quadrivecteur quantité de mouvement, Principe fondamentale de la dynamique, Travail d'une force, énergie de masse, Système de particules
5-Particules chargées dans un champ électromagnétique : Particules chargées dans un champ, électrique uniforme et constant, Particules chargées dans un champ, magnétique uniforme et constant
6-Accélérateurs de particules : Accélérateur linéaires, Accélérateur circulaires, Les cyclotrons, Les synchrocyclotrons
7-Les collisions de particules : Lois de conservation, Chaleur de réaction, Différent types de réaction, Effet Compton
Prérequis :
S6 : Mécanique Quantique
UE Mécanique quantique (16 h CM, 24h TD)
Responsable de l’enseignement
Girard Sylvain sylvain.girard@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
Prérequis :
Electromagnétisme
S5 : Ondes Electromagnétiques
UE Ondes électromagnétiques (18h CM, 22 h TD)
Responsable de l’enseignement
Colombier Jean-Philippe jean.philippe.colombier@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
1. Rappel électromagnétique : Les équations de Maxwell, Ondes planes, Le vecteur de Poynting, Ondes monochromatiques, Milieux conducteurs
2. Ondes planes sur planes interfaces : Conditions à limites, Polarisation, Les formules de Fresnel, l’angle de Brewster, Réflexion totale, effet de Goos-Haenchen, la phase de réflexion, Réflexion sur surfaces métalliques
3. Multi-couches : T matrices, Phénomènes d’interférence, Couche anti-réfléchissante, Miroir diélectrique multi-couche
4. Résonateurs et guides d’ondes : Interféromètre Fabry-Pérot, Modes d’un guide d’onde planaire, Equation de dispersion, coupure, l’indice et l’épaisseur effective
5. Faisceaux paraxiaux : Formulation de l’optique géométrique avec les matrices ABCD, Faisceaux gaussiens, passage vers systèmes optiques, Résonateurs lasers
6. Micro-ondes : Lignes de transmission, Lignes coaxiales, l’inductance, la capacité et l’impédance, Guide d’ondes rectangulaires et circulaires
Prérequis :
S3 : Electromagnétisme
S2 : Electrostatique
UE Electrostatique (12h CM, 18h TD, 9h TP)
Responsable de l’enseignement
Bahtat Mohammed Mohammed.Bahtat@univ-st-etienne.fr
Objectifs pédagogiques :
- Écrire les ordres de grandeurs des forces intervenants dans les différentes interactions fondamentales (gravitationnelle, électromagnétique, nucléaire forte et faible).
- Calculer un champ électrostatique et un potentiel électrique dans différents cas de distributions discontinues et continues de charges électriques réparties sur des figures géométriques présentant des symétries .
Syllabus :
CHARGES ELECTRIQUES
INTERRACTIONS ELEMENTAIRES :
- Loi de COULOMB (distribution de charges ponctuelles électriques – distribution continue de charges électriques.
CHAMP ELECTROSTATIQUE : - Exemples de calculs :
- Cas des charges électriques ponctuelles (exemple de deux charges ,de 3charges placées aux sommets d’un triangle, de 4 charges réparties aux sommets d’un carré .
- Cas des charges électriques réparties uniformément ou suivant une loi de distribution donnée : droite, segment de droite, surface plane ou sphérique.
POTENTIEL ELECTROSTATIQUE.ENERGIE POTENTIELLE ELECTROSTATIQUE.
RELATION GENERALE CHAMP-POTENTIEL ELECTROSTATIQUE : ( Gradient, équation de POISSON, équation de Laplace).
FLUX DU CHAMP ELECTRIQUE
THEOREME DE GAUSS : Exemples de calculs du champ électrique (cas d’un fil chargé de longueur infinie (porté par une droite) - cas d’un plan chargé - cas d’une sphère de rayon R chargée en surface ou en volume.
Prérequis :
Electricité / Electronique
S5 : Les capteurs en Physique 3 ECTS
UE Les capteurs en physique (8h CM, 12h TD, 9h TP)
Responsable de l’enseignement
Baptiste Moine baptiste.moine@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
Généralités sur les capteurs
Généralités et définitions / Capteur actifs et Passifs / Problème généraux liés à la mesure / Conditionneurs usuels / Généralités sur les convertisseurs
2-Température
Capteur de température
Capteurs à effet thermoélectrique, Peltier, Thomson / Capteurs résistifs, Thermistances / Semi-conducteur / Capteur à rayonnement infrarouge / Mise en œuvre
3-Longueurs et déplacements
Capteurs résistifs / Capteurs capacitifs / Capteurs Inductifs
TP I : Quelques éléments de métrologie
TP II : Mesure de Température
TP III : Mesure de Masse
Prérequis :
S5 : Electronique Numérique 3 ECTS
UE Electronique numérique (10 h CM, 12h TD, 12h TP)
Responsable de l’enseignement :
Pietroy David david.pietroy@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
1-Système de numération
2-Algèbre de Boole
3-Fonctions logiques de base
4-Simplification algébrique, simplification par tableau de Karnaugh
5-Logique combinatoire, additionneurs, soustracteurs, convertisseurs, multiplexeurs, codeur, décodeurs
6-Logique séquentielle, bascules, compteurs
Prérequis :
S4 : Électronique Analogique et Numérique
UE Électronique Analogique et Numérique (12h CM, 18h TD, 21h TP)
Responsable de l’enseignement
Pietroy David david.pietroy@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
Cours
• Diodes à jonction (notion sur les semiconducteurs, diodes du signal, diode zener, diode électroluminescente)
• Transistor à effet de champ (JFET, MOSFET)
• Transistor bipolaire npn, pnp, darlington.
3 TP de 4h
Transistor à effet de champ, transistor bipolaire, montages spéciaux
Prérequis :
S4 : Electronique Analogique
UE Électronique Analogique I (8h CM, 12h TD, 12h TP)
Ajouter 1 ECTS
Responsable de l’enseignement
Pietroy David david.pietroy@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
1-Notion sur l’analyse de circuits
2-Amplification, fonction de transfert, diagramme de Bode
3-Notion sur composants électroniques (diodes, transistor bipolaire, transistor à effet de champ)
4-Amplificateur opérationnel : circuits interne, Applications sur l’AOP parfait et réel en régime linéaire et de saturation
Redressement mono et double alternance, phénomènes de modulation
Prérequis :
• UE S1MIPC03, cours d'Électrocinétique
• UE S3SPI01, cours d'électricité générale
S3 : Tp physique pour l'ingénieur
UE TP de Phys. Pour l’Ingénieur (21h TP)
Responsable de l’enseignement
Emmanuel Marin : emmanuel.marin@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
Bobines à matériaux saturables 1, Bobines à matériaux saturables 2, modulation démodulation, mesures analogiques, amplificateur sélectif, machines thermiques, diodes appliquées au redressement.
Prérequis :
Physique de L1
S3 : Electricité Générale
UE Électricité Générale (8h CM, 12h TD, 21h TP)
Responsable de l’enseignement
Bahtat Mohammed Mohammed.Bahtat@univ-st-etienne.fr
Objectifs pédagogiques :
· Maitriser la représentation complexe de la loi D’OHM
· Mettre en équation un régime transitoire électrique et interprétation des solutions
Syllabus :
Induction électromagnétique.
- Expériences fondamentales : Circuit en mouvement dans un champ magnétique constant, Circuit fixe et source de champ magnétique B en mouvement, Circuit et source de champ magnétique B immobiles mais B variable, Relations quantitatives : Loi de Faraday.
- Analyses des phénomènes d’induction électromagnétique : Circuit mobile dans un champ magnétique B constant, Circuit immobile dans un champ de sources en mouvement, Circuit fixe dans un champ B variable crée par des sources fixes parcourues par I variables.
- Récapitulatif : Loi de faraday, Loi de Lenz, Quantité d’électricité induite.
- Applications immédiates : Construction de générateurs électriques, Courants de Foucault.
- Phénomènes d’auto-induction ou self-induction : Rappels et hypothèse des régimes quasi stationnaires, Courant engendré par un générateur de tension constante dans une bobine (L ,R),mise en équation et résolution, Cas où la tension E dépend du temps.
- Energie magnétique : Circuit unique, Cas de deux circuits couplés.
Courants en régimes variables
- Régimes transitoires dans un circuit RLC : Décharge d’un condensateur dans une bobine, Charge d’un condensateur à travers une bobine,
- Courants entretenus dans les circuits RLC en régime sinusoïdal : Circuit RLC série en régime sinusoïdal, Régimes sinusoïdaux étudiés au moyen des impédances complexes.
TP d'Électricité générale :
Résistances, oscilloscope+fréquencemètre, pont de Wheastone + pont en étoile, circuit RLC série, circuit bouchon, inductions magnétiques, ligne à retard
Prérequis :
· UE S2MIPC03 partie électrostatique
· UE S1MIPC03 partie électrocinétique
S1 : Electricité
UE Electricité et Analyse dimensionnelle (14hCM, 26hTD, 9h TP)
Responsable de l’enseignement
Bahtat Mohammed Mohammed.Bahtat@univ-st-etienne.fr
Objectifs pédagogiques :
- Analyser un circuit linéaire
- Faire l’analyse dimensionnelle d’un problème physique
Syllabus :
- Courant électrique: Définition, Intensité d'un courant. densité de courant, déplacement des porteurs de charge, vitesse moyenne d'entrainement des charges, relation entre I et V, relation entre I et J
- Conductivité électrique: Etude expérimentale - Loi d'Ohm (conducteur Ohmique), analyse du mécanisme de la conduction, Loi d'Ohm (synthèse) Forme intégrale et forme locale, calcul des résistances, Conducteur cylindrique homogène, conducteur homogène de section variable, association en série et en parallèle, Transformation étoile-triangle, Influence de la température
- Transfert d’énergie dans un circuit électrique – Loi d’Ohm généralisée : Energie électrique dans une portion de circuit, Cas d'un conducteur Ohmique. loi de Joules, Récepteurs non résistifs, Générateurs, Loi d'Ohm Généralisée
- Etude réseaux linéaires : Définitions, Méthode de Kirchhoff, Théorème de Thévenin, Théorème de superposition, Théorème de Millman
- Analyse dimensionnelle : Unités, équations aux dimensions, homogénéité et analyse dimensionnelle d'un problème physique
Prérequis :
Aucun
Thermodynamique
S5 : Transferts Thermiques
UE Transferts Thermiques (12h CM, 18h TD, 4h TP)
Responsable de l’enseignement :
Bahtat Mohammed mohammed.bahtat@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
1-Transfert par conduction
2-Transfert par rayonnement
3-Transfert par convection
TP Conduction Convection en régime permanent.
Prérequis :
S3 : Thermodynamique
UE Thermodynamique (16h CM, 24h TD)
Responsable de l’enseignement
Aziz Boukenter : aziz.boukenter@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
• Premier principe : Notion de système physique, Premier principe,
• Deuxième principe : Equilibre et transformation d’un système, Entropie
• Coefficients calorimétriques et thermoélastiques : Relations de Maxwell, Coefficients calorimétriques, Coefficients thermoélastiques
• Les gaz parfaits : Définitions et propriétés générales, propriétés calorimétriques des gaz parfaits, Transformation des gaz parfaits
• Machines thermiques : introduction, principe des machines thermiques, différents types de machines thermiques, cycle de Carnot, cycle de Rankine, cycle de Beau de rochas, cycle diesel, cycle de Joule
Prérequis :
Programme de Physique de L1
Mécanique
S6 Mécanique des Fluides et Acoustique
UE Mécanique des fluides et acoustique (16 h CM, 24h TD)
Responsable de l’enseignement
Bahtat Mohammed mohammed.bahtat@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
Mécanique des fluides
1-Statique des fluides
2-Cinématique (description de Lagrange et description d’Euler)
3-Dynamique des fluides (équation de Navier-stockes)
4-Théorème de Bernoulli et applications
5-Théorème de Bernoulli généralisé
6-Théorème de la quantité de mouvement
Acoustique
1-Rappels sur la propagation : Qu’est-ce qu’un phénomène de propagation ?, Équation de propagation, Qu’est-ce qu’une onde ?, Résolution de l’équation de propagation, Onde plane, Ondes progressives, Ondes stationnaires
2-Ondes sonores dans les fluides : généralités, Équation de propagation; Approximations acoustiques, Vitesse du son dans les fluides, Aspects énergétiques, Réflexion/transmission, L’effet Doppler
Prérequis :
S5 Mécanique des milieux continues
UE Mécanique du Solide et des milieux Continus (12 CM, 18 TD, 4 TP)
Responsable de l’enseignement
Yvan Chalamet yvan.chalamet@univ-st-etienne.fr
Objectifs pédagogiques :
L'objectif du cours de Mécanique des milieux continus est d'élaborer la généralisation de la mécanique rationnelle aux milieux continus et d'en déduire les lois de conservation et de comportement. Le contenu du cours s'articule comme suit: la cinématique des milieux continus, la dynamique des milieux continus et les lois de comportement classique.
Syllabus :
1. Cinématique : Tenseurs de déformation de Cauchy-Green, Tenseurs de déformation de Green-Lagrange, Tenseurs de déformation d’Euler-Armansi, Tenseurs de déformation infinitésimale
2. Dynamique : Théorème de transport de Reynolds, Conservation de la masse, Tenseur de contrainte de Gauchy, Conservations de la quantité de mouvement et du moment cinétique
3. Energétique : Conservation de l’énergie totale, Conservation de l’énergie interne, Conservation de l’énergie cinétique, Inégalité de Clausius-Duhem, Energie libre spécifique de Helmholtz
4. Lois de comportement : Principe de base, Fluide visqueux newtonien, solide élastique linéaire
5. Mécanique des fluides : Equations de Navier-Stokes pour un fluide parfait, Equation de Navier-Stokes pour les fluides incompressibles
6. Mécanique du solide : Equations de Navier pour un solide élastique linéaire isotrope en petite déformation
7. Transfert Thermique : Conduction de chaleur, Thermodynamique du gaz idéal
Prérequis :
cours de « Modélisation mathématique pour la physique et la mécanique » du S4 ou cours à option du S5 (obligatoire pour les étudiants venant de l'IUT: « Remise à niveau en mathématique »
S4 : Ondes Scalaires
UE Onde Scalaires (12h CM, 18h TD) Ajout de TP ??
Responsable de l’enseignement
Lafon Éric eric.lafon@univ-st-etienne.fr
Objectifs pédagogiques :
Le cours vise à faire comprendre les aspects universels du mouvement oscillatoire dans le domaine de la mécanique des vibrations linéaires.
À la fin du cours, et pour atteindre les objectifs généraux, l’étudiant devra être capable de :
1ère période
• décrire un mouvement harmonique simple amorti ou non, à un degré de liberté
• modéliser un système oscillant à un degré de liberté soumis à des frottements secs ou fluides,
• définir les concepts d’oscillations libres amorties ou non,
• appliquer les équations différentielles linéaires du second ordre, homogène, à coefficients constants, à la résolution de phénomènes oscillatoires à un degré de liberté, libres ou forcées.
• définir le concept de résonance et analyser les paramètres qui le caractérisent
• résoudre les équations différentielles décrivant des mouvements sinusoidaux forcées à l’aide des nombres complexes
• traiter le regime forcé périodique non sinusoïdal en appliquant les séries de Fourier à la décomposition d’un signal périodique d’excitation
2ème période
• décrire un système couplé à deux degrés de liberté à travers les notions de formes propres
• appliquer les outils de l’algèbre linéaire à la résolution d’équations différentielles couplées dans le cadre des systèmes libres et conservatifs à 2 , 3 et n degrés de liberté
• analyser, justifier et argumenter les caractéristiques d’un système couplé avec un oscillateur secondaire permettant de canaliser les effets de résonance d’amplitude lors d’excitations forcées sinusoidales
• comparer, critiquer tout type de graphique de systèmes oscillants en réponse temporelle ou spectrale pour argumenter des valeurs des paramètres déterminant (frequence de résonance, fréquence propre, bande passante, coefficient de frottement, facteur d’amplification).
• reconnaître et analyser un système résonant dans tt autre domaine de la physique tel que l’électrocinétique, l’optique, l’acoustique, la mécanique des fluides à travers les quelques concepts fondamentaux introduits
Syllabus :
• L’oscillateur élémentaire linéaire
• Le régime libre de l’OEL : conservatif, dissipatif
• Le régime permanent harmonique de l’OEL
• Le régime permanent périodique de l’OEL
• Le régime forcé de l’OEL
• L’oscillateur forcé en optique : l’origine de la dispersion
• Systèmes linéaires à 2 degrés de liberté
Prérequis :
- • UE S2MIPC23, cours de Cinématique et Dynamique
S3 : Mécanique du Solide
UE Mécanique du Solide (8h CM, 12h TD)
Responsable de l’enseignement
Yvan Chalamet : yvan.chalamet@univ-st-etienne.fr
Objectifs pédagogiques :
• Expliquer les principes de bases des lois de la mécanique classique
• Appliquer les principes de bases des lois de la mécanique classique à des problèmes de calculs d’efforts ou de mouvements de systèmes solides indéformables.
Syllabus :
• CINÉMATIQUE
o NOTION DE MOUVEMENT
o NOTIONS DE VITESSE
o ACCÉLÉRATION
• ACTIONS MÉCANIQUES
• ACTIONS MÉCANIQUES
• ÉLÉMENTS DE CINÉTIQUE
o CARACTÉRISTIQUES MÉCANIQUES D’UN SOLIDE
o QUANTITÉS DE MOUVEMENT ET D’ACCÉLÉRATION
• ÉNERGIE CINÉTIQUE
• PRINCIPE FONDAMENTAL DE LA DYNAMIQUE « PFD »
o ÉNONCÉ DU PFD.
o RÉFÉRENTIELS GALILÉENS
o ÉQUATIONS PRINCIPALES D’UN PROBLÈME
S2 : Cinématique et Dynamique du Point
UE Cinématique et Dynamique (14h CM, 26h TD, 9h)
Responsable de l’enseignement
Baptiste Moine baptiste.moine@unvi-st-etienne.fr
Objectifs pédagogiques :
- Décrire les différents aspects d’un mouvement complexe d’un point
- Faire le lien entre les forces agissant sur un objet ponctuel et le mouvement résultant en utilisant les lois fondamentales de la dynamique
- Modéliser la situation donnée d'un corps pour en décrire son mouvement ou le champ de forces auquel il est soumis.
Syllabus :
Cinématique
- Introduction
- Coordonnées d’un point – trajectoire : Repère cartésien, Repère cylindrique, Repère sphérique, Trièdre de Frenet – Serret, Rayon de courbure
- Vitesse d’un point : Repère cartésien, cylindrique, Frénet
- Accélération : Repère cartésien, cylindrique, Frénet (composantes tangentielle et normale)
- Exemples de mouvements simples : rectilignes, sinusoïdal, circulaire, abscisse curviligne, mouvement cycloïdal…
- Changement de référentiel : Mouvement relatif et mouvement absolu
- Loi de composition des vitesses
- Loi de composition des accélérations
- Cas particuliers de rotation pure (autour d’un axe)
- Application à l’étude du mouvement de rotation de la terre
Dynamique
- Principes et définitions
- Référentiels d’inertie
- Force
- Principe fondamental de la dynamique et applications
- Limites de validités de la relation fondamentale (référentiel terrestre)
- Théorèmes généraux : Moment cinétique, Force centrale
- Energie : Théorème de l’énergie cinétique, Force conservative, Energie potentielle
- Lien force et énergie potentielle
- Energie mécanique totale
- Relations entre énergie et équilibre
Prérequis :
Aucun
Optique
S6 : Vision
UE Vision (12h CM, 18h TD)
Responsable de l’enseignement
Alain Tremeau alain.tremeau@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
1-Principes de base de la Vision humaine
2-Vision artificielle : Eclairage, Types d’image, Optique, Capteur, Calibrage, Unité de traitement
3-Traitement d’image
4-Mise en œuvre
Prérequis :
S5 : Interférence et Diffraction
UE Interférences diffraction (12h CM, 18h TD, 12h TP)
Responsable de l’enseignement
Destouches Nathalie nathalie.destouches@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
Interférences
1-Interférences à deux ondes : ondes planes, ondes sphériques
2-Conditions d’interférence : cohérence temporelle, cohérence spatiale
3-Interféromètres à division de front d’onde : l’expérience d’Young, les autres interféromètres
4-Interféromètres à division d’amplitude : films diélectriques (interférence à deux ondes), franges d’égale inclinaison, franges d’égale épaisseur, interféromètre de Michelson, autres interféromètres
5-Interférences à ondes multiples : calculs généraux, en réflexion et en transmission, coefficient de finesse, fonction d’Airy, interféromètre de Fabry-Pérot, ensemble de source cohérentes, réseau de N fentes infiniment fines éclairées par une onde plane cohérente en incidence normale ou oblique
Diffraction
1-Principe d’Huygens-Fresnel
2-Diffraction de Fresnel et Fraunhofer
3-Diffraction de Fraunhofer par différents types d’ouvertures : rectangulaire, fente, circulaire, résolution des systèmes optiques, l’expériende des fentes d’Young en tenant compte de la largeur des fentes, le réseau de fentes
Prérequis :
S4 : Ondes, Propagation et Polarisation
UE Ondes, Propagation et polarisation
(12h CM, 18h TD, 12h TP)
Responsable de l’enseignement
Destouches Nathalie nathalie.destouches@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
1. Ondes : Ondes unidimensionnelles, L’équation d’onde différentielle, Les ondes harmoniques, Phase et vitesse de phase, Le principe de superposition, La représentation complexe, Phaseur et addition d’ondes, Ondes planes, L’équation d’onde différentielle tri-dimensionnelle, Les ondes sphériques
2. Ondes électromagnétiques. Introduction aux équations de Maxwell : De l’électrostatique aux équations de Maxwell, L’équation d’onde, Energie, Les équations de Maxwell dans un milieu homogène, linéaire isotrope, diélectrique, non dispersif en l’absence de charges et de courants libres, Cas particulier des ondes harmoniques, Les équations de Maxwell satisfaites par des ondes monochromatiques, Expression de l’intensité pour des ondes monochromatiques, Ondes transverses, Expression de l’intensité pour une onde plane monochromatique, Les ondes aux interfaces : relations de passage
3. Ondes optiques : Qu’est-ce que la lumière ?, Introduction des différentes théories optiques, Modèle scalaire des ondes optiques, Expression générale, Onde plane, Onde sphérique, Emission lumineuse et notions de cohérence, Propagation de la lumière, Principe de Huygens, Etablissement des lois de la réfraction à partir du principe de Huygens, Superposition de deux ondes cohérentes de même fréquence, Addition de deux ondes cohérentes de fréquences différentes mais voisines
4. Polarisation, Biréfringence : Lumière polarisée, Nature électromagnétique de la lumière, Etude générale de l’état de polarisation, Les différents états de polarisation, Dispositifs polarisants, Polarisation par réflexion vitreuse, Formules de Fresnel pour les matériaux diélectriques, Polarisation par dichroïsme avec films de polymères (Polaroïds), Polarisation par biréfringence, Polarisation par diffusion, Polariseurs et loi de Malus, Biréfringence, Milieux isotropes et anisotropes, Matériaux uniaxes, Biréfringence, Lames cristallines, Lames cristallines particulières, Mesure de l’anisotropie d’une lame cristalline, Pouvoir rotatoire et activité optique
TP Onde et polarisation
• Réflexion en Lumière polarisée
• Loi de malus
• Introduction aux interférence et à la diffraction
Prérequis :
• UE S1MIPC03, cours d'optique géométrique
S1 : Optique géométrique
UE Optique Géométrique (12h CM, 18h TD, 9h)
Responsable de l’enseignement
Youcef Ouerdane ouerdane@univ-st-etienne.fr
Objectifs pédagogiques :
Syllabus :
Cours d' Optique Géométrique :
Introduction : Longueur d’onde, fréquence, de vibration et vitesse de propagation, indice de réfraction d’un matériau
Rayon lumineux : Concept de base et propriétés
Réflexion – Réfraction de la lumière : Lois
Principe de Fermat
Image d’un point lumineux formée par un système optique
Miroir plan
Stigmatisme
Objet réel (virtuel) – image réelle (virtuelle)
Image d’un objet plan perpendiculaire à l’axe optique
Aplanétisme : Condition des sinus d’Abbe
Grandissement transverse
Dioptre sphérique
Image d’un point de l’axe et invariant fondamental
Stigmatisme approché et conditions de Gauss
Relation de conjugaison : Origine au centre et au sommet et aux foyers
Foyers d’un dioptre et distance focale
Vergence
Construction d’une image (cas de dioptre convergent – divergent) : Construction de rayons réfractés, Grandeur de l’image
Miroir plan et miroir sphérique
Lentilles minces : Définitions, Image d’un point de l’axe, Différents types de lentilles, Image d’un objet plan perpendiculaire à l’axe : Cas de lentille convergente et divergente, Formules de conjugaison
Association de lentilles accolées
Instruments d’optique : Systèmes centrés, Définitions, Foyers, Plans principaux, Exemples
Construction géométriques des rayons et des images
Associations de systèmes centrés
Prérequis :
Aucun