realizată de Emma Paterson 3 ani în urmă
253
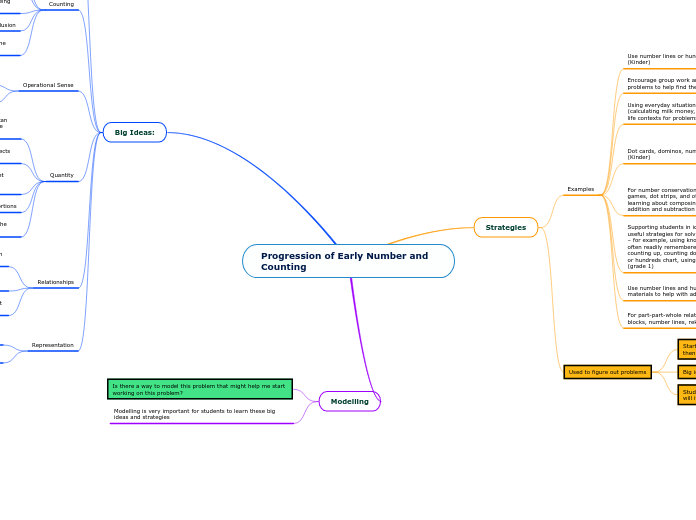
Progression of Early Number and Counting
Engaging young learners in mathematics involves a variety of strategies and tools to support their understanding of numbers and counting. For early grades like kindergarten and first grade, using dot cards, dominos, and dice can help children develop subitizing skills, which are foundational for estimation.