4 Validez del Modelo
Comprueba si el modelo propuesto hace en realidad lo que dice que hace, es decir, ¿predice adecuadamente el comportamiento del sistema que se estudia? Al principio, el equipo de IO debe estar convencido de que el resultado del modelo no contenga “sorpresas”. En otras palabras, ¿tiene sentido la solución? ¿Los resultados son intuitivamente aceptables? Del lado formal, un método común de comprobar la validez de un modelo es comparar su resultado con resultados históricos. El modelo es válido si, en condiciones de datos de entrada iguales, reproduce de forma razonable el desempeño pasado. Sin embargo, no suele haber seguridad de que el desempeño futuro continuará copiando el comportamiento pasado. Además, como el modelo se basa en el
examen cuidadoso de datos pasados, la comparación propuesta casi siempre es favorable.
Si el modelo propuesto representara un sistema nuevo (inexistente), no habría datos históricos disponibles. En esos casos podemos utilizar la simulación como una herramienta independiente para comprobar el resultado del modelo matemático.
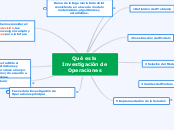
Qué es la Investigación de Operaciones
Fases de la Investigación de Operaciones principal
Los estudios de investigación de operaciones se basan en la labor de equipo, donde los analistas de IO y el cliente trabajan codo con codo. Los conocimientos de modelado de los analistas de IO se deben complementar con la experiencia y cooperación del cliente
para quien realizan el estudio.
Como herramienta de toma de decisiones, la IO es tanto una ciencia como un arte. Es una ciencia por las técnicas matemáticas que incorpora, y un arte porque el éxito de las fases que conducen a la solución del modelo matemático depende en gran medida de la creatividad y experiencia del equipo de IO.Willemain (1994) manifiesta que “una práctica [de IO] eficaz requiere más que competencia analítica. También requiere, entre otros atributos, juicio técnico (es decir, cuándo y cómo utilizar una técnica dada), así como habilidades de comunicación y supervivencia organizacional”.
Es difícil prescribir cursos de acción específicos (semejantes a los que indica la teoría precisa de la mayoría de los modelos matemáticos) para estos factores intangibles.
Sin embargo, podemos ofrecer lineamientos generales para la implementación de la IO en la práctica.
Para implementar la IO en la práctica, las fases principales son:
1. Definición del problema.
2. Construcción del modelo.
3. Solución del modelo.
4. Validación del modelo.
5. Implementación de la solución.
¿Qué debemos considerar previamente?
1. Antes de aventurarse en un complicado modelado matemático, el equipo de IO debe explorar la posibilidad de utilizar ideas “agresivas” para resolver la situación.
La solución del problema de los elevadores con la instalación de espejos se basó en la psicología humana más que en el modelado matemático. También es más sencilla y menos costosa que cualquier recomendación que un modelo matemático pudiera haber producido. Quizás esta sea la razón de que los equipos de investigación de operaciones suelan recurrir a los conocimientos de personas “externas” que se desempeñan en campos no matemáticos (el psicológico en el caso del problema de los elevadores).
2. Las soluciones se originan en las personas y no en la tecnología. Cualquier solución que no tome en cuenta el comportamiento humano probablemente falle.
3. Un estudio de IO no debe iniciar con el prejuicio de utilizar una herramienta matemática específica antes de que se justifique su uso. Por ejemplo, como la programación lineal es una técnica exitosa, existe la tendencia de utilizarla para modelar “cualquier” situación. Esa forma de proceder suele conducir a un modelo matemático del todo alejado de la situación real. Por lo tanto, es imperativo que se analicen primero los datos disponibles aplicando las técnicas más simples siempre que sea posible
(por ejemplo, promedios, gráficas e histogramas), para determinar el origen del problema.
Una vez que se define el problema, puede decidirse cuál será la herramienta más apropiada para la solución.
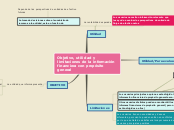
La toma de decisión es factible si satisface todas las restricciones y además es óptima si produce el mejor valor (Máximo o mínimo) de acuerdo a lo buscado en el problema
Para su análisis debemos considerar: las alternativas de decisión, las restricciones que nos exigen cumplir y los criterios objetivos para la futura toma de decisión
Rama de la Ingeniería Industrial consistente en el uso de modelo matemáticos, algoritmicos y estadísticos.
- Las primeras actividades formales de investigación de operaciones (IO) se iniciaron en Inglaterra durante la Segunda Guerra Mundial, cuando un equipo de científicos empezó a tomar decisiones con respecto a la mejor utilización del material bélico. Al término de la guerra, las ideas formuladas en operaciones militares se adaptaron para mejorar la eficiencia y productividad en el sector civil.
- La terminología básica de la IO, que comprende el modelado matemático, soluciones factibles, optimización y cálculos iterativos. Hace hincapiéen que la definición correcta del problema es la fase más importante (y más difícil) depracticar la IO.
- También se recalca que si bien el modelado matemático es la piedra angularde la IO, en la decisión final se deben tomar en cuenta factores incuantificables,como el comportamiento humano.
Subtema
5 Implementación de la Solución
Implica la transformación de los resultados en instrucciones de operación comprensibles que se emitirán a las personas que administrarán el sistema recomendado. La responsabilidad de esta
tarea recae principalmente en el equipo de IO.
3 Solución del Modelo
Es por mucho la más sencilla de todas las fases de IO porque
implica el uso de algoritmos de optimización bien definidos. Un aspecto importante de la fase de solución del modelo es el análisis de sensibilidad. Tiene que ver con la obtención de información adicional sobre el comportamiento de la solución óptima cuando el modelo experimenta algunos cambios de parámetros. El análisis de sensibilidad es particularmente necesario cuando no se pueden estimar con precisión los parámetros del modelo. En estos casos es importante estudiar el comportamiento de la solución óptima en el entorno de los parámetros estimados.
2 Construcción del Modelo
La construcción del modelo implica un intento de transformar la definición del problema en relaciones matemáticas. Si el modelo resultante se ajusta a uno de los modelos matemáticos estándar, como la programación lineal, se suele obtener una solución utilizando
los algoritmos disponibles. Por otra parte, si las relaciones matemáticas son demasiado complejas como para permitir la determinación de una solución analítica, el equipo de IO puede optar por simplificar el modelo y utilizar un método heurístico, o bien considerar la simulación, si es lo apropiado. En algunos casos, una simulación matemática puede combinarse con modelos heurísticos para resolver el problema de decisión.
1 Definición del Problema
Implica definir el alcance del problema investigado. Esta función debe ser realizada por todo el equipo de IO. El objetivo es identificar tres elementos principales del problema de decisión: (1) descripción de las alternativas de decisión; (2) determinación del objetivo del estudio, y (3) especificación de las limitaciones bajo las cuales funciona el sistema modelado.