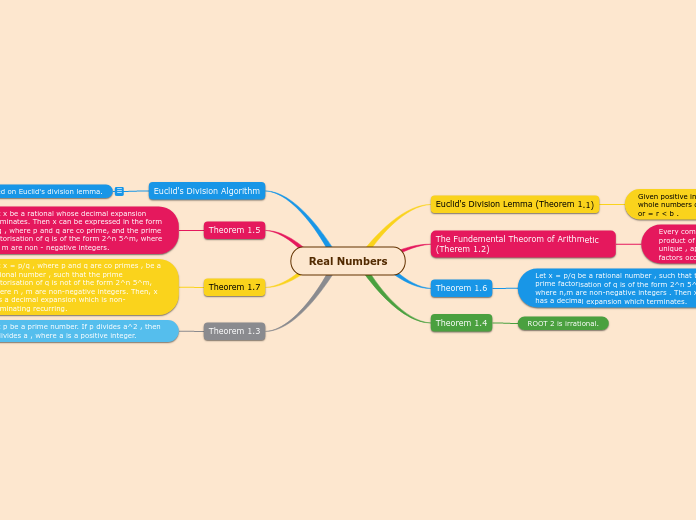
Real Numbers
Theorem 1.3
Let p be a prime number. If p divides a^2 , then p divides a , where a is a positive integer.
Theorem 1.7
Let x = p/q , where p and q are co primes , be a rational number , such that the prime factorisation of q is not of the form 2^n 5^m, where n , m are non-negative integers. Then, x has a decimal expansion which is non-terminating recurring.
Theorem 1.5
Let x be a rational whose decimal expansion terminates. Then x can be expressed in the form p/q , where p and q are co prime, and the prime factorisation of q is of the form 2^n 5^m, where n , m are non - negative integers.
Euclid's Division Algorithm
this is based on Euclid's division lemma.
According to this the HCF of any 2 positive integers a and b , with a>b , is obtained as follows:
Step 1 : Apply the division lemma to find q and r where a=bq+r, 0 , or = r < b.
Step 2 : If r=0, the HCF is b. If r is not equal to 0 , apply Euclid's lemma to b and r.
Step 3 : Continue the process till the remainder is zero . The divisor at this stage will be HCF (a,b). Also , HCF (a,b) = HCF (b,r) .
Theorem 1.4
ROOT 2 is irrational.
Theorem 1.6
Let x = p/q be a rational number , such that the prime factorisation of q is of the form 2^n 5^m, where n,m are non-negative integers . Then x has a decimal expansion which terminates.
The Fundemental Theorom of Arithmetic (Therem 1.2)
Every composite number can be expressed as a product of primes, and this factorisation is unique , apart from the order in which the prime factors occur.
Euclid's Division Lemma (Theorem 1.1)
Given positive integers a and b , there exists
whole numbers q and r satisfying a = bq + r , 0< or = r < b .