Argomenti di laboratorio
I sistemi visti in laboratorio sono retroazionati, perché il funzionamento dei macchinari dipende non solo da input esterni, ma anche da input che provengono da sensori che riflettono lo stato della macchina.
Tuttavia questi sistemi non sono analizzabili con la trasformata di Laplace, perché non sono lineari.
Retroazione
Cos'è un sistema retroazionato?
Un sistema retroazionato è un sistema in cui l'output viene monitorato continuamente e utilizzato a sua volta come input. Questo richiede la presenza di un percorso chiuso sul sistema (che dall'output torna all'input). Per questo si parla di sistemi ad anello chiuso (closed loop), per distinguerli da quelli ad anello aperto (open loop). Il collegamento dall'uscita all'ingresso viene detto "ramo di retroazione". La parte del sistema che elabora gli input per ottenere l'output è invece detto "catena diretta".
Altre definizioni relative a questo contesto:
Setpoint: nel contesto del problema della regolazione* (nel quale si vuole assegnare un valore costante all'uscita) l'ingresso viene detto setpoint. Esso è il valore che corrisponde a un certo valore dell'uscita desiderato. (*il problema della regolazione si distingue da quello del controllo, in cui l'ingresso varia continuamente nel tempo).
Segnale di errore: nel contesto dei sistemi studiati (che riguarda i sistemi lineari con retroazione negativa) al segnale di ingresso (setpoint) viene sottratto il segnale di uscita per ottenere il segnale di errore, come differenza tra valore desiderato e valore reale. (questo è rigorosamente vero solo se nel ramo di retroazione la fdt vale 1, come in molti degli esempi visti in classe).
Funzione di anello: è il prodotto tra la fdt della catena diretta e la fdt del ramo di retroazione. Tutti i vantaggi della retroazione che sono stati discussi dipendono dal fatto di avere un modulo elevato della funzione di anello. Anche il criterio di Bode dipende da questa funzione. Per queste ragioni essa merita un nome particolare.
Perché viene utilizzata la retroazione nei sistemi automatici?
Perché se le condizioni di lavoro di un macchianario cambiano, ma il setpoint rimane lo stesso, è desiderabile che il sistema si porti comunque verso il valore desiderato.
Esempio spesso ripetuto in classe: se imposto la velocità di rotazione a vuoto di un trapano/tornio in un sistema a catena aperta, mi accorgerò che questa scende drasticamente quando vado a fare la lavorazione (per esempio un foro). Per ripristinare la velocità dovrei intervenire manualmente. Il ramo di retroazione permette invece che il punto di lavoro tenda a tornare verso il setpoint senza interventi esterni (cioé in maniera automatica).
Vantaggi della retroazione
Riduzione dell'effetto della variazione dei parametri: posso dimensionare il sistema perché abbia certe prestazioni e una certa fdt. Quando vado a scegliere dei componenti reali non troverò mai dei pezzi che abbiano esattamente i parametri calcolati e questo porta il sistema ad avere una fdt diversa. Questo effetto viene ridotto se la funzione di anello è elevata (ma solo se i parametri che cambiano si trovano nella catena diretta!).
Riduzione dell'effetto dei disturbi: simile al precedente. Tutti i sistemi reali risentono di disturbi esterni (di tipo elettrico, mecanico o altro). L'impatto di questi disturbi viene ridotto se il modulo della funzione di anello è elevato (ma solo se i disturbi si trovano nella catena diretta!).
Allargamento della banda: in presenza i retroazione negativa e fdt elevata il sistema retroazionato è più veloce (tempo di salita ridotto) di quello a catena aperta.
Stabilizzazione: a differenza di altri modi di connettere dei sistemi (in serie o parallelo) la retroazione ha l'effetto di spostare i poli della fdt equivalente. Di conseguenza può modificare il sistema dal punto di vista della stabilità.
Sistemi di retroazione al di fuori del contesto tecnologico:
https://youtu.be/odCtXFpOz3Q
La retroazione non riguarda solo le macchine, ma è presente in molti fenomeni naturali (sistemi ecologici, clima, ...), economici e sociali.
In genere la presenza di un anello di retroazione negativa aiuta il sistema ad autoregolarsi; un anello di retroazione positiva tende a portare il sistema lontano dall'equilibrio iniziale. Possono essere presenti contemporaneamente più anelli di tipo diverso. A seconda del caso possono prevalere gli effetti della retroazione negativa oppure quelli della retroazione positiva.
Tipi di sistema ed errori a regime
Che cosa si intende con sistemi di tipo 0, 1 e 2?
I sistemi di tipo 0,1 e 2 sono sistemi retroazionati con funzione H(s), in particolare, si parla di:
- Sistemi di tipo 0: se la funzione di anello G(s)H(s) non ha poli nell'origine;
- Sistemi di tipo 1: se la funzione di anello G(s)H(s) ha 1 polo nell'origine;
- Sistemi di tipo 2: se la funzione di anello G(s)H(s) ha 2 poli nell'origine.
NB: Un polo si ha quando il denominatore assume valore 0.
In cosa si differenziano i sistemi di tipo diverso?
Si differenziano per i valori assunti dagli errori di posizione, velocità e accelerazione.
Qual è il ruolo particolare dei poli in una f.d.t.?
Stabilità
Criteri di stabilità
Basati sulla posizione dei poli:
- sistema asintoticamente stabile se: tutti i poli hanno parte reale negativa;
- sistema semplicemente stabile: poli a parte reale negativa e poli semplici (non multipli) a parte reale nulla;
- sistema instabile: almeno un polo a parte reale positiva oppure poli multipli a parte reale nulla.
Basati sulla risposta impulsiva (utile per collegamento con integrali impropri):
- condizione necessaria alla stabilità (semplice oppure asintotica) è che la risposta impulsiva tenda a zero;
- condizione necessaria e sufficiente alla stabilità asintotica è che l'area della risposta impulsiva sia finita;
Criterio di Bode:
Se entrambi i margini di un sistema (Margine di fase e Margine di guadagno) sono positivi allora si può dire che il sistema in questione è asintoticamente stabile
Definizioni
Stabilità asintotica: Un sistema è asintoticamente stabile se e solo se, utilizzando il teorema del valore finale, si tende ad un valore pari a zero
Stabilità semplice: Un sistema è semplicemente stabile se, utilizzando il teorema del valore finale, si ha una tendenza finita ma non pari a zero
Instabilità: Un sistema è instabile se, utilizzando il teorema del valore finale, il risultato tende a infinito
Stabilità BIBO (Bounded Input Bounded Output): a un ingresso limitato in ampiezza corrisponde un uscita limitata in ampiezza. ESEMPIO DI SISTEMA NON BIBO STABILE: la funzione di trasferimento 1/s (è la fdt che integra il segnale di ingresso) non è BIBO stabile perché per un ingresso a gradino (ingresso di ampiezza limitata) la sua uscita è una rampa che tende a infinito (non ha ampiezza limitata).
Relazioni tra definizioni:
- BIBO e asintotica sono equivalenti;
- asintotica/BIBO implica stabilità semplice (di un sistema asintoticamente stabile si può dire che anche semplicemente stabile);
Teorema del valore iniziale:
Da inserire la formula del teorema del valore iniziale
Teorema del valore finale:
Da inserire la formula del teorema del valore finale
Risposta dinamica
Cosa si intende quando si parla di "risposta dinamica"?
Quando si parla di risposta dinamica si fa riferimento all'andamento nel tempo dell'uscita di un sistema sollecitato dagli ingressi canonici (impulso, gradino, rampa,...). Per esempio osservando l'andamento della risposta al gradino posso trarre informazioni sulla velocità del sistema, sul suo coefficiente di smorzamento, ecc...
Quali sono i parametri caratteristici di una risposta al gradino?
Tempo di salita, tempo di assestamento, massima sovraelongazione, tempo di picco.
Risposta all'impulso: che cos'è?
Risposta all'impulso: che legame ha con la stabilità di un sistema?
Esiste una relazione tra risposta al gradino e risposta in frequenza? Quale?
Perché usare la risposta dinamica di un sistema quando la risposta in frequenza rappresenta già in pratica una descrizione completa del sistema?
Sistemi del primo e del secondo ordine
Definizione di ordine di un sistema:
Parametri di un sistema del primo ordine: tau (1/tau = pulsazione del polo). Mi dà informazioni sulla velocità del sistema:
- tau grande -> sistema lento; ragionando in frequenza si può dire che la banda passante è più stretta (perché si estende fino alla pulsazione del polo 1/tau)
- tau piccola -> sistema veloce; ragionando in frequenza si può dire che la banda passante è più larga (perché si estende fino alla pulsazione del polo 1/tau)
Parametri di un sistema del secondo ordine:
- coefficiente di smorzamento
- pulsazione naturale.
Questi sono in relazione (tramite delle formule che non serve ricordare) con alcune caratteristiche significative della risposta al gradino.
In pratica parto da delle specifiche sulla risposta dinamica (per esempio quella al gradino: voglio limitare la sovraelongazione al 10%, il tempo di assestamento a 1 secondo, ...) e da esse ricavo coefficiente di smorzamento e pulsazione naturale.
Il passaggio successivo è quello di scegliere i componenti (R, L, C; massa, molla, smorzatore) che realizzano quella funzione di trasferimento.
Trasformata di Laplace
Qual è la sua definizione? (utile per fare un collegamento con gli integrali impropri)
link alla pagina di wikipedia.
f(t) è la funzione che si vuole trasformare. Il risultato è una funzione della variabile complessa s.
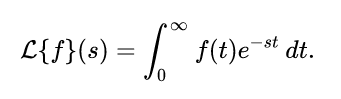
A cosa serve?
La sua utilità pratica è quella di semplificare il calcolo dei transitori dei segnali di uscita dei sistemi lineari.
Il calcolo dei transitori richiederebbe la soluzione di equazioni differenziali (equazioni in cui l'incognita è una funzione).
Tramite la trasformata di Laplace il problema si riduce alla soluzione di un'equazione algebrica.
Di fatto, utilizzando questo strumento, un sistema può essere descritto tramite il rapporto tra l'uscita e l'ingresso. Questo rapporto è detto "funzione di trasferimento" del sistema (vedi il nodo relativo nella mappa concettuale).
Teoremi e proprietà
Linearità: ℒ[ Af(t) + Bg(t)] = A F(s) + B G(s)
Teoremi del valore iniziale e finale.
Derivazione: se ℒ[f(t)] = F(s) allora ℒ[f'(t)] = s F(s)
Integrazione: si ottiene dal precedente. La trasformata dell'integrale si ottiene dividendo F(s) per s.
Funzione di trasferimento
sistemaQual è la sua espressione per i sistemi lineari?
Una funzione razionele fratta, cioè un rapporto tra polinomi nella variabile s. Dall'espressione della f.d.t. posso ricavare zeri e poli, uguagliando numeratore (per gli zeri) e denominatore (poli) a zero.
Che relazione ha con la risposta in frequenza?
La risposta in frequenza è la funzione di trasferimento ristretta all'asse immaginario. In pratica ottengo la risposta in frequenza sostituendo jw a s.
Come si rappresentano graficamente gli zeri ed i poli?
Poli e zeri sono numeri complessi e quindi si rappresentano nel piano di Gauss. Indico gli zeri con o e i poli con x.
Che cosa rappresenta?
È il rapporto tra le trasformate di Laplace del segnale di uscita e del segnale di ingresso di un sistema, e per questo descrive il comportamento del sistema.
A cosa serve? Come la utilizzo?
Il suo uso si ricollega a quello della trasformata di Laplace (calcolare il transitorio della risposta di un sistema). In pratica, se conosco la funzione di trasferimento F(s) e l'espressione dell'ingresso x(t), posso calcolare l'uscita y(t) seguendo i seguenti passaggi:
- calcolo la trasformata di Laplace di X(s) = ℒ[ x(t)] (in genere posso farlo utilizzando senza applicare la definizione della trasformata ma semplicemente consultando la tavola delle trasformate, da sinistra verso destra);
- calcolo la trasformata dell'uscita moltiplicando X(s) ed F(s): Y(s) = X(s)F(s);
- ricavo y(t) antitrasformando Y(s) (utilizzando la tavola delle trasformate, da destra verso sinistra). Spesso, in questa fase, è necessario ricorrere alla scomposizione in fratti semplici (é per questo motivo che molte tavole con le trasformate riportano nella seconda colonna solo frazioni con polinomi di grado 1 o 2, perché se il grado fosse superiore potrei utilizzare la scomposizione in fratti semplici).
Risposta in frequenza
Che significato ha la risposta in frequenza?
La risposta in frequenza è una funzione matematica che descrive come un sistema si comporta al variare della frequenza del segnale di ingresso applicato.
Più precisamente si tratta di una funzione complessa di variabile reale: il suo argomento è la pulsazione ω (che va pensata come la pulsazione di un segnale sinusoidale applicato all'ingresso del sistema) e il suo valore è un numero complesso che rappresenta come la sinusoide viene amplificata e sfasata dal sistema.
In pratica la risposta in frequenza è il rapporto tra l'uscita (sinusoidale) e l'ingresso (sinusoidale) rappresentati come numeri complessi.
ESEMPIO: se un sistema è descritto dalla risposta in frequenza F(jω) e questa risposta vale 3+4j (modulo = 5 e fase = atan(4/3) = 37°) per ω = 10 rad/s, questo significa che se l'ingresso è
x(t) = 3 sin(10t)
allora l'uscita è
y(t) = 15 sin (10t + 53°)
E se il segnale in ingresso non è sinusoidale? Posso interpretare la risposta in frequenza nello stesso modo? Per esempio, se l'ingresso è un'onda quadra posso usare la risposta in frequenza per calcolare come essa viene attenuata (o amplificata) e sfasata?
Le informazioni che ottengo dalla risposta in frequenza sono relative ad ingressi sinusoidali e non sono valide per segnali di forma diversa.
Se voglio utilizzare la risposta in frequenza con ingressi di tipo diverso, devo:
- rappresentare questi ingressi come somma di sinusoidi (le cui frequenze saranno multiple intere di quella fondamentale);
- applicare le sinusoidi singolarmente;
- sommare gli output ottenuti (sovrapposizione degli effetti).
In genere la forma d'onda in uscita risulterà distorta rispetto a quella in ingresso (basta pensare al circuito RC che si usa per verificare la carica del condensatore: in ingresso ho un'onda quadra, in uscita gli andamenti di carica e scarica).
Qual è la sua espressione per i sistemi lineari (cioè per il tipo di sistemi visti. In pratica sono i sistemi per cui vale il principio di sovrapposizione)?
Per i sistemi lineari l'espressione della risposta in frequenza è un rapporto tra polinomi nella variabile (jω).
Come si rappresenta graficamente?
Si rappresenta tramite i diagrammi d Bode.
Che relazione ha con la trasformata di Laplace?
La trasformata di Laplace è una generalizzazione della risposta in frequenza, che permette di analizzare non solo il comportamento sinusoidale ma anche il comportamento in corrispondenza di ingressi qualsiasi. La risposta in frequenza è un caso particolare della trasformata di Laplace.
Dal punto di vista matematico la risposta in freqenza si ottiene a partire dalla trasformata di Laplace sostituendo al suo argomento (la variabile complessa s) il numero immaginario jω.
Esiste un legame tra risposta in frequenza e risposta dinamica?
Diagrammi di Bode
A cosa servono?
Servono a rappresentare graficamente la risposta in frequenza.
Come si leggono?
In corrispondenza di una pulsazione (in ascissa) leggo (nelle ordinate) l'attenuazione e lo sfasamento della sinusoide in uscita rispetto a quella di ingresso (alla pulsazione scelta)
Tracciamento: quali sono le regole di tracciamento per i sistemi lineari?
I fattori che compaiono nella risposta in frequenza di un sistema lineare sono solo cinque: costante; zero o polo nell'origine; zero o polo al finito. Basta tacciare separatamente il contributo di ciascuno di questi fattori e poi sommarli tra di loro.
Tracciamento: perché è possibile considerare i fattori della risposta in frequenza separatamente e poi sommarli nel grafico?
Perché per i moduli si usano i dB come unità di misura. Essendo i dB il risultato del calcolo di un logaritmo, si applica la proprietà per cui il logaritmo del prodotto è pari alla somma dei logaritmi dei singolii fattori.
Per le fasi la possibilità deria da una proprietà dei numeri complessi (nel prodotto le fasi si sommano).
Definizioni di decade e ottava:
Per decade si intende un intervallo di pulsazioni che ha un'ampiezza unitaria nella scala logaritmica in base 10. Oppure: è un intervallo di frequenze (o pulsazioni) i cui estremi stanno in rapporto 1:10.
Es. ω e 10ω; 500 Hz e 5 kHz
Per ottava si intende un intervallo di pulsazione (o frequenza) i cui estremi stanno in rapporto 1:2 (uno doppio dell'altro).
Es. ω e 2ω; 500 Hz e 1 kHz
Quali legami ci sono tra diagrammi di Bode e la stabilità di un sistema?
In base al teorema di Bode sappiamo che un sistema si può ritenere stabile se entrambi i margini (di fase e di guadagno) sono positivi.
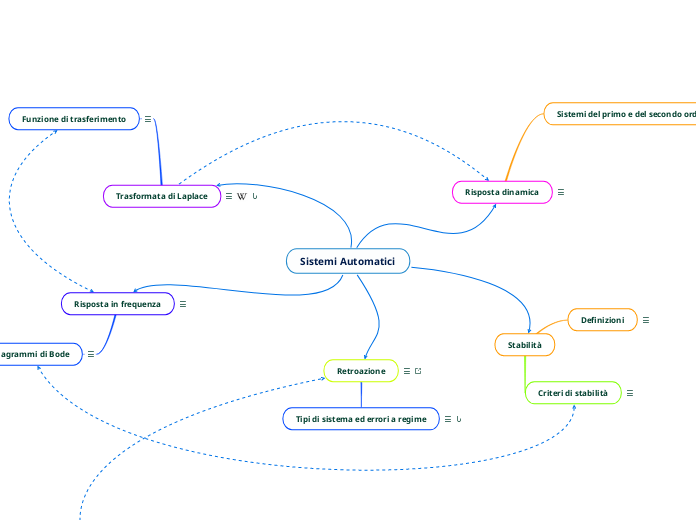
Sistemi Automatici