по Rhys Bowie 3 лет назад
273
Algebra!!!
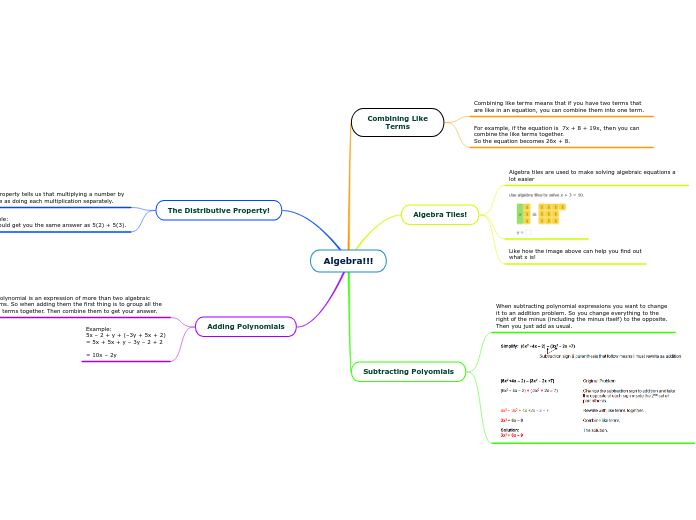
Understanding algebra involves several key concepts, including combining like terms, using the distributive property, and handling polynomials. Combining like terms means merging terms with the same variables in an equation, such as turning 7x + 19x into 26x.