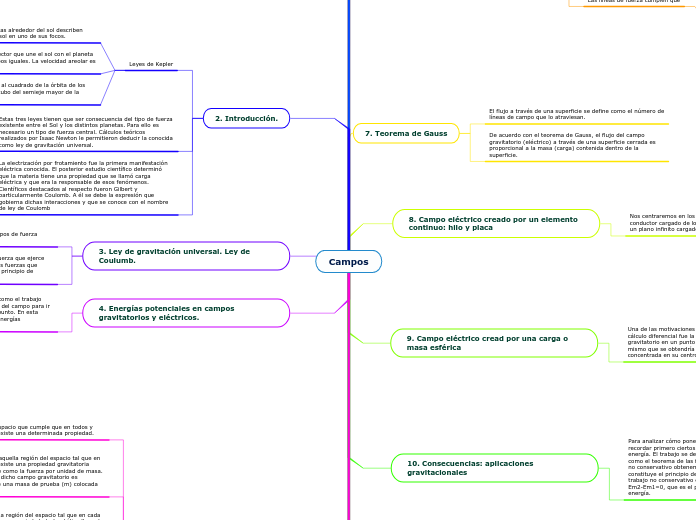
Campos
5. Vector intensidad de campo. Concepto de potencial
Conclusiones
Las cargas negativas van a potenciales crecientes.
Las cargas positivas se desplazan espontáneamente hacia potenciales decrecientes
Llamaremos campo escalar al campo en el que su magnitud representativa es un escalar.
El potencial también cumple el principio de superposición y la relación entre el campo y el potencial es que el campo es la derivada primera del potencial cambiada de signo E = - dV/dx.
El potencial en un punto de un campo eléctrico es igual numéricamente a la energía potencial que posee la unidad de carga positiva, por estar situada en ese punto.
El potencial en un punto de un campo gravitatorio se define como la energía potencial gravitatoria que posee la unidad de masa (1 Kg) colocada en dicho punto.
Campo eléctrico es aquella región del espacio tal que en cada uno de sus puntos existe una propiedad electrostática llamada E y que se define como la fuerza por unidad de carga.
El campo gravitatorio es aquella región del espacio tal que en cada uno de sus puntos existe una propiedad gravitatoria llamada g y que se define como la fuerza por unidad de masa. Para poner de manifiesto dicho campo gravitatorio es necesario la existencia de una masa de prueba (m) colocada en dichos puntos.
Una característica importante del campo gravitatorio es que los cuerpos que se mueven bajo la acción exclusiva de un campo gravitatorio experimentan una aceleración que no depende ni del material ni del estado físico del cuerpo. De hecho, g es la intensidad de campo gravitatorio y la aceleración de la gravedad. Esto es debido a que la misma cualidad del cuerpo se interpreta como inercia o gravedad según las circunstancias.
Campo es la región del espacio que cumple que en todos y cada uno de sus puntos existe una determinada propiedad.
4. Energías potenciales en campos gravitatorios y eléctricos.
La energía potencial en un punto se define como el trabajo cambiado de signo realizado por las fuerzas del campo para ir desde el origen de potenciales hasta dicho punto. En esta descripción supondremos que el origen de energías potenciales es el infinito.
3. Ley de gravitación universal. Ley de Coulumb.
En una distribución arbitraria de cargas la fuerza que ejerce una carga sobre otra es independiente de las fuerzas que ejerzan las demás. Éste es el enunciado del principio de superposición
Los campos gravitatorio y eléctrico son campos de fuerza centrales y, por tanto, conservativos.
2. Introducción.
La electrización por frotamiento fue la primera manifestación eléctrica conocida. El posterior estudio científico determinó que la materia tiene una propiedad que se llamó carga eléctrica y que era la responsable de esos fenómenos. Científicos destacados al respecto fueron Gilbert y particularmente Coulomb. A él se debe la expresión que gobierna dichas interacciones y que se conoce con el nombre de ley de Coulomb
Estas tres leyes tienen que ser consecuencia del tipo de fuerza existente entre el Sol y los distintos planetas. Para ello es necesario un tipo de fuerza central. Cálculos teóricos realizados por Isaac Newton le permitieron deducir la conocida como ley de gravitación universal.
Leyes de Kepler
3ª Ley de Kepler: El período al cuadrado de la órbita de los planetas es proporcional al cubo del semieje mayor de la órbita descrita
2ª Ley de Kepler: El radio vector que une el sol con el planeta barre áreas iguales en tiempos iguales. La velocidad areolar es constante
1ª Ley de Kepler: Los planetas alrededor del sol describen órbitas elípticas, estando el sol en uno de sus focos.
1. Repaso de mecánica. Momento de una fuerza. Momento angular.
La Mecánica es un cuerpo de conocimientos que estudia los procesos físicos desde el punto de vista cinemático, dinámico y energético
La Dinámica es una teoría basada en las ideas de masa y fuerza. Describe los fenómenos naturales utilizando las tres leyes de Newton que relacionan la aceleración de un cuerpo con su masa y las fuerzas que sobre él actúan.
Por tanto, el enunciado de la segunda ley de Newton para la rotación será: La derivada respecto al tiempo del momento angular de una partícula es igual al momento de la fuerza que actúa sobre ésta
En el caso de que dicha fuerza tenga la misma dirección que el vector de posición, el momento de la fuerza es cero y el momento angular es constante
El momento angular de un cuerpo permanece constante si sobre él no actúan fuerzas o las fuerzas que actúan son centrales. Por lo tantp, la trayectoria de un punto material que se mueve bajo la acción de una fuerza central es siempre plana.
Para definir el estado de movimiento de un cuerpo que describe un movimiento curvilíneo, se utiliza el concepto de momento cinético o momento angular. L= r x p
El momento de una fuerza es el agente dinámico de la rotación, del mismo modo que la fuerza lo es de la traslación. Se define como M=r x F
Como producto vectorial, el vector momento es perpendicular a los vectores posición y fuerza, y su módulo es el área del paralelogramo que determinan ambos vectores.
Para definir el estado de movimiento de un cuerpo mientras se traslada, se utiliza el concepto de cantidad de movimiento o momento lineal el cual se define como:
El momento lineal de un cuerpo es una magnitud vectorial, de la misma dirección y sentido que la velocidad, y cuyo valor es igual al producto de la masa del cuerpo por la velocidad que éste posee.
A partir de la cantidad de movimiento, podemos reformular las tres leyes de la dinámica (leyes de Newton)
2º Ley: Si la fuerza o resultante de fuerzas es nula, el momento lineal es constante. Esto constituye el principio de conservación del momento lineal
3ª ley: El principio de acción-reacción en términos de momento lineal se expresa como Δpa=Δpb
Leyes de Newtown
- 1ª ley: Si no se aplican fuerzas sobre un cuerpo este sigue su estado de movimiento (MRU) o reposo
- 2º ley: F=m x a
- 3ª ley: Principio de acción-reacción: las fuerzas actúan siempre por pares; si un objeto A ejerce sobre otro objeto B una fuerza, B ejerce sobre A otra fuerza igual en módulo y dirección, pero de sentido opuesto.
La fuerza es toda magnitud física capaz de deformar un cuerpo o de modificar su estado de reposo o movimiento, o ambas a la vez.
11. Consecuencias: Aplicaciones electrostáticas
Cuando dos conductores se cargan con cargas opuestas y su posición relativa es tal que todas las líneas de campo que nacen del conductor positivo mueren en el negativo, decimos que tenemos un condensador
En la práctica se emplean dispositivos abiertos, tales como el condensador plano.
Cuando un conductor se carga con una carga q adquiere un potencial V, y la validez del principio de superposición garantiza que, si la carga se duplica, también lo hará el potencial. Esto es, la carga y el potencial de un conductor son proporcionales, q = C·V
La conservación de la carga puede ilustrarse mediante un método simple de cargar un conductor llamado carga por inducción.
Un dipolo eléctrico está formado por dos cargas eléctricas separadas una distancia r. Esta distribución de cargas se representa mediante un vector, el momento dipolar eléctrico,
d = q x r, dirigido desde la carga negativa a la positiva.
10. Consecuencias: aplicaciones gravitacionales
Para analizar cómo poner satélites en órbita, debemos recordar primero ciertos conceptos importantes acerca de la energía. El trabajo se define como W=ΔEc, que se conoce como el teorema de las fuerzas vivas. Despejando el trabajo no conservativo obtenemos que Wnc=Em2-Em1, que constituye el principio de la conservación de energía, si el trabajo no conservativo es 0, podemos determinar que
Em2-Em1=0, que es el principio de conservación de la energía.
El trabajo total para poner en órbita un satélite es la suma del trabajo de llevarlo hasta una cierta altura sobre la superficie terrestre y el trabajo de hacerlo orbitar. Dado que el trabajo de los motores es un trabajo debido a una reacción química, se trata de trabajo no conservativo.
Generalizando, podemos decir que el trabajo para poner en órbita un satélite es el trabajo de subir el satélite hasta su órbita, más el trabajo de hacerlo orbitar. Una vez arriba, la energía total del satélite será la suma de su energía cinética más su energía potencial
9. Campo eléctrico cread por una carga o masa esférica
Una de las motivaciones que tuvo Newton para desarrollar el cálculo diferencial fue la de demostrar que el campo gravitatorio en un punto exterior de una esfera maciza es el mismo que se obtendría si toda la masa de la esfera estuviera concentrada en su centro.
8. Campo eléctrico creado por un elemento continuo: hilo y placa
Nos centraremos en los casos del campo creado por un hilo conductor cargado de longitud infinita y del campo creado por un plano infinito cargado uniformemente.
7. Teorema de Gauss
De acuerdo con el teorema de Gauss, el flujo del campo gravitatorio (eléctrico) a través de una superficie cerrada es proporcional a la masa (carga) contenida dentro de la superficie.
El flujo a través de una superficie se define como el número de líneas de campo que lo atraviesan.
6. Representación del campo: Líneas del campo y superficies equipotenciales
Las líneas de fuerza cumplen que
- Van de cargas positivas a cargas negativas.
- Simetría alrededor de las cargas.
- Número proporcional a la carga creadora del campo.
- Densidad proporcional al módulo del campo eléctrico.
- A suficiente distancia el comportamiento equivale a la carga neta.
- Las líneas de campo nunca se cortan.
Como todo campo de fuerzas, el campo gravitatorio y el campo eléctrico se representan mediante líneas de campo y superficies equipotenciales.
Las cargas positivas son fuentes del campo y las cargas negativas son sumideros
Las masas son sumideros del campo
Las representaciones de los campos escalares utilizan las denominadas superficies equipotenciales, que se definen como las superficies que contienen todos los puntos con el mismo valor del potencial.
Las representaciones de los campos vectoriales utilizan las denominadas líneas de campo, que se definen de modo que en cada punto son tangentes al vector campo en dicho punto.