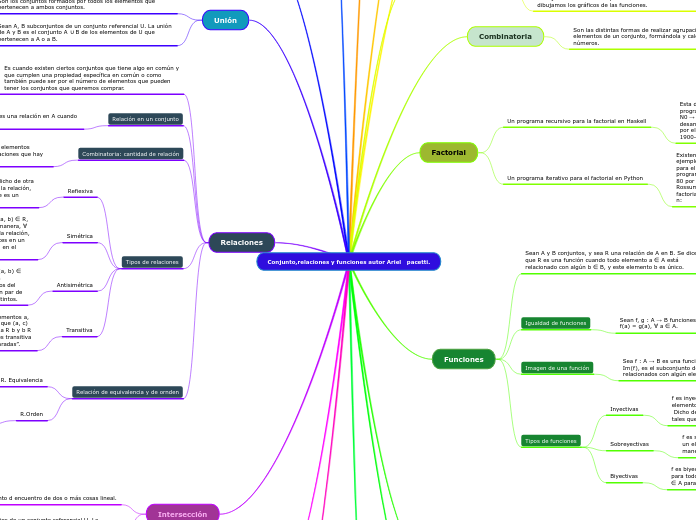
Conjunto,relaciones y funciones autor Ariel pacetti.
Cardinal de un conjunto
Sea A un conjunto, se llama cardinal de A a la cantidad de elementos distintos que tiene A, y se nota #A. Cuando el conjunto no tiene un número finito de elementos, se dice que es infinito, y se nota #A = ∞
#∅ = 0, #{a, b, c} = 3 = #{1, 2, 3}, #N = ∞. Notar que, si A es un conjunto finito, #A ∈ N ∪ {0} =N_0.
Operaciones entre conjuntos
La unión de dos conjuntos A y B es el conjunto A ∪ B que contiene todos los elementos de A y de B.
P = {n ∈ N : n es un número par }, o I = {x ∈ R : x ≤ 2} = [−∞, 2), que no es lo mismo que J = {x ∈ N : x ≤ 2} = {1, 2}.
Intersección
Sean A, B subconjuntos de un conjunto referencial U. La intersección de A y B es el conjunto A ∩ B de los elementos de U que pertenecen tanto a A como a B.
A ∩ B = {c ∈ U : c ∈ A y c ∈ B} o también c ∈ A ∩ B ⇐⇒ c ∈ A y c ∈ B.
Es el punto d encuentro de dos o más cosas lineal.
Sean A = {1, 2, 3, 5, 8}, B = {3, 4, 5, 10} ⊆ U = {1, . . 10}. Entonces A ∩ B = {3, 5}.
Relaciones
Relación de equivalencia y de ornden
R.Orden
Se dice que R es una relación de orden cuando es una relación reflexiva, antisimétrica y transitiva.
R. Equivalencia
Las relaciones de equivalencia juegan un rol muy importante en matemática, porque de algún modo funcionan como una generalización de la igualdad. Se dice que R es una relación de equivalencia cuando es una relación reflexiva, simétrica y transitiva.
Tipos de relaciones
Transitiva
Se dice que R es transitiva si para toda terna de elementos a, b, c ∈ A tales que (a, b) ∈ R y (b, c) ∈ R, se tiene que (a, c) ∈ R también (dicho de otra manera, ∀ a, b, c ∈ A, a R b y b R c ⇒ a R c). En términos del grafo de la relación, R es transitiva si hay un “camino directo” por cada “camino con paradas”.
Antisimétrica
Se dice que R es antisimétrica si cada vez que un par (a, b) ∈ R con a ≠ b, entonces el par (b, a) ∈ R/ (dicho de otra manera, ∀ a, b ∈ A, a R b y b R a ⇒ a = b). En términos del grafo de la relación, R es antisimétrica si no hay ningún par de flechas en sentidos opuestos que unen dos vértices distintos.
Simétrica
Se dice que R es simétrica si cada vez que un par (a, b) ∈ R, entonces el par (b, a) ∈ R también (dicho de otra manera, ∀ a, b ∈ A, a R b ⇒ b R a). En términos del grafo de la relación, R es simétrica si por cada flecha que une dos vértices en un sentido, hay una flecha (entre los mismos vértices) en el sentido opuesto.
Refiexiva
Se dice que R es reflexiva si (a, a) ∈ R, ∀ a ∈ A (dicho de otra manera, a R a, ∀ a ∈ A). En términos del grafo de la relación, R es reflexiva si en cada vértice hay una flecha que es un “bucle”, es decir que parte de el y llega a el.
Combinatoria: cantidad de relación
Sean A_m y B_n conjuntos finitos, con m y n elementos respectivamente. Entonces la cantidad de relaciones que hay de A_m en B_n es igual a 2^(m∙n)
Relación en un conjunto
Sea A un conjunto. Se dice que R es una relación en A cuando R ⊆ A × A.
Las relaciones R6 y R7 arriba son relaciones en el conjunto R. La igualdad de elementos siempre es una relación en cualquier conjunto A: R = {(a, a), a ∈ A}, es decir ∀ a, b ∈ A : a R b ⇔ a = b.
Es cuando existen ciertos conjuntos que tiene algo en común y que cumplen una propiedad específica en común o como también puede ser por el número de elementos que pueden tener los conjuntos que queremos comprar.
Sean A = {a, b, c}, B = {1, 2}. Entonces R1 = {(a, 1),(b, 1),(b, 2)}, R2 = {(a, 2),(b, 2),(c, 1),(c, 2)}, R3 = ∅ y R4 = A × B son ejemplos de relaciones de A en B, y R5 = {(1, c),(2, a)} es un ejemplo de relación de B en A (notar que importa el orden).
Unión
Sean A, B subconjuntos de un conjunto referencial U. La unión de A y B es el conjunto A ∪ B de los elementos de U que pertenecen a A o a B.
A∪B = {c ∈ U : c ∈ A y c ∈ B} o también ∀ c ∈ U, c ∈ A∪ B ⇐⇒ c ∈ A o c ∈ B.
Son los conjuntos formados por todos los elementos que pertenecen a ambos conjuntos.
Si A = {1, 2, 3, 5, 8} y B = {3, 4, 5, 10} ⊆ U = {1, . . ., 10} entonces A ∪ B = {1, 2, 3, 4, 5, 8, 10}.
Complemento
Sea A subconjunto de un conjunto referencial U. El complemento de A (en U) es el conjunto A′ de los elementos de U que no pertenecen a A.
A ′ = {b ∈ U : b /∈ A}, o también ∀ b ∈ U, b ∈ A ′ ⇐⇒ b /∈ A.
Es un conjunto que contiene todo los elementos que no se encuentran en el conjunto original.
• Si U = {1, 2, 3} y A = {2}, entonces A′ = {1, 3}.
• Se tiene ∅ ′ = U y U ′ = ∅.
• (A′ ) ′ = A.
Informal de un conjunto y elementos
El orden de los elementos no importa en un conjunto y no se tiene en cuenta las repeticiones de los elementos. Se dice que cada elemento a de un conjunto A pertenece al conjunto A, y se nota a ∈ A. Si un objeto b no pertenece al conjunto A, se nota b ɇ A.
Sea A = {1, 2, 3}: 1 ∈ A, 2 ∈ A, 4 ∈/ A, {1, 2} ɇ A, ∅ ɇ A.
Sea B = {2, {1}, {2, 3}}: {1} ∈ B, {2, 3} ∈ B, 1 ɇ B, 3 ɇ B.
Un conjunto es una colección de objetos,llamados elementos, que tiene la propiedad que dado un objeto cualquiera se puede decidir si ese objetos es del conjunto o no.
ℤ = {. . ., −2, −1, 0, 1, 2, . . .} el conjunto de los números enteros.
ℕ = {1, 2, 3, 4, . . .} el conjunto de los números naturales.
Tablas de verdad de la lógica proposicional.
Tabla de verdades de los conectores lógicos
Es una tabla que muestra el valor de verdad de una proposición compuesta, para cada combinación de valores de verdad que se pueda asignar a sus componentes. para establecer un sistema formal se establecen las definiciones de los operadores.
Conjunto de partes
Es el conjunto de todo los subconjunto de un conjunto.
• Sea A = {1, 2, 3}: P(A) = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, A}.
• Cualquiera sea el conjunto A, ∅ ∈ P(A), A ∈ P(A).
• P(∅) = {∅}, o sea el conjunto que tiene como único elemento al conjunto vacío.
Diferencia simétrica
Tabla de valores
Es el conjunto de elementos que solo pertenecen a A o a B pero no a ambos a la vez.
• Sean A = {1, 2, 3, 5, 8}, B = {3, 4, 5, 10} ⊆ U = {1, . 10}. Entonces A △ B = {1, 2, 4, 8, 10}.
• Sean I = (−∞, 2], J = [−10, 10) ⊆ U = R. Entonces I △ J = [−∞, −10) ∪ (2, 10].
Funciones
Tipos de funciones
Biyectivas
f es biyectiva si es a la vez inyectiva y sobreyectiva, es decir para todo elemento b ∈ B existe exactamente un elemento a ∈ A para el cual f(a) = b.
Sobreyectivas
f es sobreyectiva si para todo elemento b ∈ B existe al menos un elemento a ∈ A para el cual f(a) = b. Dicho de otra manera, f es sobreyectiva si Im(f) = B.
Inyectivas
f es inyectiva si para todo elemento b ∈ B existe a lo sumo un elemento a ∈ A para el cual f(a) = b.
Dicho de otra manera, f es inyectiva si para todo a, a′ ∈ A tales que f(a) = f(a ' ) entonces a = a ' .
Imagen de una función
Sea f : A → B es una función. La imagen de f, que se nota Im(f), es el subconjunto de elementos de B que están relacionados con algún elemento de A.
Im(f) = {b ∈ B : ∃ a ∈ A tal que f(a) = b}.
Sea f2 : N → N, f2(n) = n+ 1. Entonces Im(f2) = N≥2 pues para todo m ≥ 2, existe n ∈ N tal que n + 1 = m (tomando n = m − 1 que pertenece a N pues m ≥ 2) pero 1 ∈/ Im(f2) pues no existe n ∈ N tal que n + 1 = 1.
Igualdad de funciones
Sean f, g : A → B funciones. Se dice que f = g cuando f(a) = g(a), ∀ a ∈ A.
Dada una función f : A → B, el conjunto A se llama el dominio de la función f, y el conjunto B se llama el codominio de la función f. Como se ve de los ejemplos anteriores, todos los elementos del dominio tienen que estar involucrados en una función, pero puede ocurrir que haya elementos del codominio que no estén involucrados.
Sean A y B conjuntos, y sea R una relación de A en B. Se dice que R es una función cuando todo elemento a ∈ A está relacionado con algún b ∈ B, y este elemento b es único.
Es decir
∀ a ∈ A, ∃ ! b ∈ B : a R b. Aquí el símbolo “∃ !” significa “existe un ´único”
es decir: ∀ a ∈ A, ∃ b ∈ B tal que a R b, y si b, b′ ∈ B son tales que a R B y a R b ′ , entonces b = b ′ .
Como a cada a ∈ A le corresponde un b ∈ B y este b es único, se le puede dar un nombre que hace notar la dependencia de a: se dice que b es la imagen de a por f, y se suele notar “b = f(a)”.
La relación del conjunto A = {1, 2, 3, 4, 5} en el conjunto B = {1, 4, 7, 23} descrita por el diagrama siguiente es una función.
Factorial
Un programa iterativo para el factorial en Python
Existen otros lenguajes de programación no funcionales, por ejemplo, imperativos. Si escribimos un programa iterativo para el factorial en el extensamente usado lenguaje de programación imperativo Python, creado a fines de los años 80 por el computador y matemático holandés Guido van Rossum, resulta más parecido a la primer definición de factorial que dimos como el producto de todos los enteros ≤ n:
def factorial(n)
f = 1
for i in range (1, n + 1) :
f = f ∗ i
return f
Un programa recursivo para la factorial en Haskell
Esta definición recursiva está muy en sintonía con la programación funcional. Por ejemplo la función factorial: N0 → N en el lenguaje de programación funcional Haskell, desarrollado a partir de mediados de los 80, y nombrado así por el matemático y lógico americano Haskell Brooks Curry, 1900-1982.
Se define de la siguiente manera
• Factorial:: Integer → Integer
• Factorial 0 = 1
• Factorial n = n ∗ factorial(n − 1)
Combinatoria
Son las distintas formas de realizar agrupaciones con los elementos de un conjunto, formándola y calculando los números.
Sea A es un conjunto finito y sea B ⊆ A. Entonces #B ≤ #A.
Este método nos sirve para los conjuntos infinitos.
Producto cartesiano
El nombre producto cartesiano fue puesto en honor al maten ático, físico y filósofo francés
René Descartes, 1596-1650. El plano euclídeo R
2 = {(x, y); x, y ∈ R} representado mediante
Los ejes cartesianos es el plano donde constantemente dibujamos los gráficos de las funciones.
Si A = B = R, entonces R × R es el espacio euclídeo R^2 .
Proposición
Sean A, B, C conjuntos dentro de un conjunto referencial U.
Entonces
Leyes distributivas
A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) y A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
Leyes De Morgan 1806-1871
1871 (A ∪ B) ′ = A ′ ∩ B ′ y (A ∩ B) ′ = A ′ ∪ B ′ .
es una afirmación con sentido completo, y constituye la forma más elemental de la lógica. Las proposiciones brindan información sobre un acontecimiento falsable, es decir, que puede ser falso o verdadero.
La tierra es plana.
Igualdad de conjunto
Se dice que dos conjuntos son iguales si tienen exactamente los mismos elementos. Una forma práctica para saber si dos conjuntos son iguales lo que hay que hacer es determinar si se contiene uno al otro.
A = B ⇐⇒ A ⊆ B y B ⊆ A
Es decir, A = B si tienen exactamente los mismos elementos (sin importar el orden y sin tener en cuenta repeticiones de elementos). (Aquí, el símbolo “⇔” es el símbolo de la bi-implicación, que se lee “si y sólo si”.
Subconjuntos e inclusión
Sea A un conjunto. Se dice que un conjunto B está contenido en A, y se nota B ⊆ A (o también B ⊂ A), si todo elemento de B es un elemento de A. En ese caso decimos también que b está incluido en A, o que B es un subconjunto de A. Si B no es un subconjunto de A se nota B ̸⊆ A (o B ȼ A).
Ejemplo
• Sea A = {1, 2, 3}: {1} ⊆ A, {2, 3} ⊆ A, ∅ ⊆ A, A ⊆ A, {3, 4} ̸⊆ A.
• A ⊆ A y ∅ ⊆ A cualquiera sea el conjunto A.
O sea, B está incluido en A si para todo b, se tiene que si b pertenece a B entonces b pertenece a A, y B no está incluido en A si existe b perteneciendo a B tal que b no pertenece a A. Maten áticamente se escribiría así:
B ⊆ A si ∀ b, b ∈ B ⇒ b ∈ A , B ̸⊆ A si ∃ b ∈ B : b ȼ A.