Importancia de los procesos de Pensamiento Lógico para el Currículo Escolar Colombiano

Больше похоже на это

QUÉ ES PENSAR?

от emily castro

Ciencias Cognitivas y/o Teorías pedagógicas en la educación no convencional

от Misael Pacheco

ARIADNA: Red de programas y proyectos del IES Miguel Catalán

от Marta Delgado

características básicas de los protocolos

от Joel Castillo

Importancia de los procesos de Pensamiento Lógico para el Currículo Escolar Colombiano

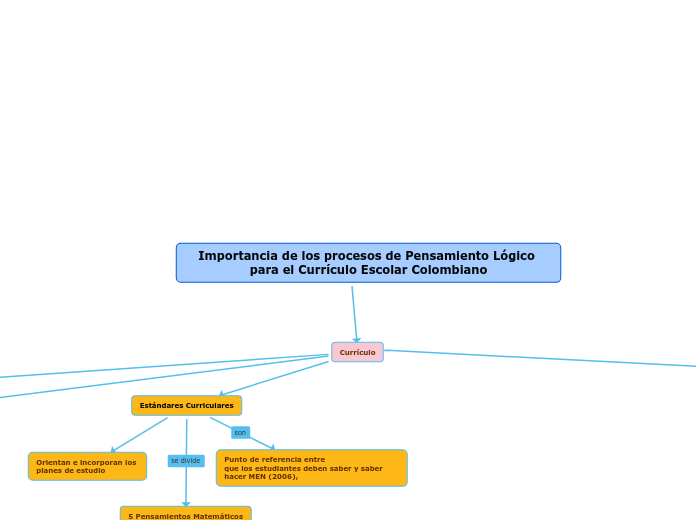
Currículo

Estándares Curriculares

5 Pensamientos Matemáticos

Pensamiento Espacial y Sistemas Geométricos

Construir y manipular conceptos y representaciones

Estudiar las formas geométricas y características

Comprender la realidad del estudiante

involucrar al estudiante en situaciones para tomar decisiones de azar o situaciones lógicas

Pensamiento Variacional y Sistemas Algebraicos Analíticos

involucrar al estudiante en situaciones para reconocer e identificar la variabilidad

Pensamiento Métrico y Sistemas de Medida

Comprender la manipulación de medidas y cantidades

la medición y uso de sistemas métricos

Comprender las propiedades de magnitudes

solucionar situacioens

Pensamiento Numérico y Sistemas Numéricos

Comprender el concepto del número

Las operaciones y sus aplicaciones

Propiedades de los sistemas numéricos

Punto de referencia entre que los estudiantes deben saber y saber hacer MEN (2006),

Orientan e incorporan los planes de estudio

Lineamientos Curriculares

Ordenar y Apoyar el PEI

Que el estudiante viva las amtematicas

intercambiar información y experiencias

Guía orientadora para observar las enseñanzas dentro del aula educativa MEN (1998)

Contexto

Situaciones Problema

Autonomia

Adaptación

Buen trabajo

Valor Universal

Parte del contexto y generan apendizaje

Parte de las fases de aprendizaje

Ver la iimportancia matemática

Usar la matemática

Ser Creativo

Ser Mediador

Ambientes que rodean al estudiante

Diseñar y ejecutar estrategias didácticas

Intervenir, modificar y enriquecer el contexto

Pensamiento Matemático

Pensamiento Variacional

Dominar conceptos

Cuantificar variaciones por cantidades y magnitudes

Modelos matemáticos

Cambio relativo

Cambio absoluto

Aplicativa

Aditiva

Álgebra

Magnitudes

Dependencia y modelo función

Continua numérica

Logro de la educación básica

Pensamiento Aleatorio

Una situación de datos

Resolver problemas

Relacionar el Currículo

Solucionar situaciones matemáticas

Pensamiento Métrico

Construir conceptos de magnitud

Comprender procesos de conservación de magnitudes

Estimar y apreciar magnitudes

Seleccionar unidades de medida, patrones e instrumentos

Diferenciar la unidad y el patrón de medición

Pensamiento Espacial

Representar y manipular información

Explorar y reflexionar el espacio

Construir y manipular representaciones mentales de objetos del espacio

Pensamiento Númerico

Una comprensión general de los números y las operaciones

Evolucionar en contextos significativos

Reflexionar resultados matemáticos

Comprender los números y la numeración

Comprender las operaciones

Adquiere con influencias del contexto

Procesos Matemáticos

Resolución y Planteamiento de Problemas

Un Objetivo primario de enseñanza

Formular problemas con situaciones dentro y fuera de matemáticas

Desarrollar y aplicar estrategias para resolver problemas

Verificar e interpretar resultados

Generalizar soluciones y estrategias para los problemas

Confianza en el uso significativo de las matemáticas

Comparación y Ejercitación de Procedimientos

Conocimiento de actuaciones, destrezas, estrategias, métodos, técnicas, usos y aplicaciones

Resolver actos de manera precisa

Facilitar la aplicación matemática

Generalidades diversas

Geométrico

Rutinas para construir y manipular un modelo geométrico

Analítico

Hace referencia al álgebra, funciones y cálculo diferencial e integral

Procedimientos de rutina

Medir

Identificar atributos medibles de un objeto o figura

Transformar

Cambio formal para un nuevo objeto matemático

Graficar

Construir gráficas mediante cálculos

Calcular

Efectuar operaciones para llegar a un resultado

Métrico

Emplear las magnitudes longitud, tiempo, amplitud, capacidad, peso y superficie.

Aritmetico

Dominar el sistema de numeración decimal y de las 4 operaciones básicas

Modelación

Brindar una imagen simplificada

Identificar las matemáticas en un contexto general

Esquematizar

Formular y visualizar un problema

Descubrir relaciones y regularidades

Transferir problemas al mundo matemático

Comunicación

Habilidad para comunicarse

Construir vínculos entre las nociones y el lenguaje abstracto y simbólico de las matemáticas

Expresar ideas de diferentes formas.

Comprender, interpretar y evaluar ideas

Construir, interpretar y ligar ideas o relaciones

Observar, formular preguntas, reunir y evaluar información

Producción y presentación de argumentos

Razonamiento

Ordenar ideas para llegar a una conclusión.

Dar cuenta del cómo y del porqué para llegar a conclusiones.

Justificar las estrategias y procedimientos de problemas.

Formular hipotesis y posibles soluciones

Encontrar patrones y expresarlos

Argumentos propios para exponer ideas

Estructura fundamental de las instituciones

Requiere de docentes flexibles y activos

Mantener la tarea docente-alumno y alumno-docente

Un conjunto de criterios, planes de estudio, metodologías y procesos

Permite aprender el arte de educar y enseñar

Dan una formación integral y construcción cultural nacional, regional y local

Desarrollan en el proyecto educativo institucional