по Michael Gomez 3 лет назад
440
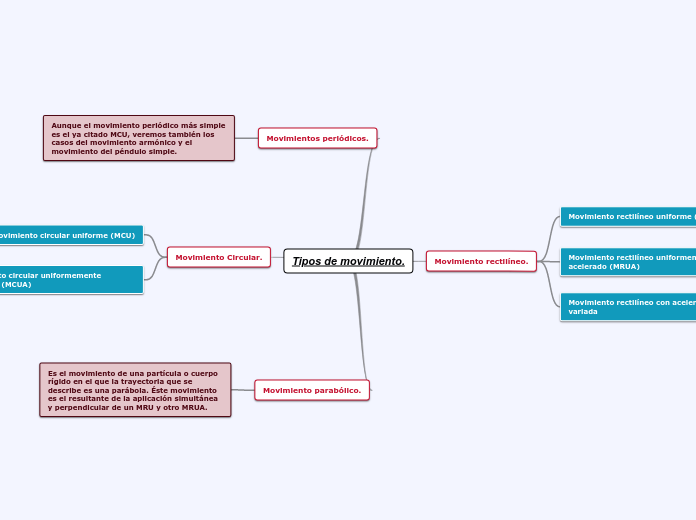
MOVIMIENTO CIRCULAR
El movimiento circular uniformemente variado (MCUV) se caracteriza por tener una trayectoria curva y una velocidad que varía. Este tipo de movimiento incluye aceleración centrípeta, tangencial y angular.