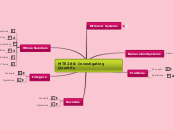
MTE 280: Investigating Quantity
Decimals
Addition:
When adding decimals, you line up the numbers by place value. For example, 4.22 + 3.5 would be shown as:
4.22
+3.5
--------
7.72
Multiplication of decimals:
.4 x 2 = .8
For this problem, you could draw a figure that has ten pieces with four of them shaded. You would do this twice. Then, you would count how many you have, which is 8 tenths or .8.
Using Base Ten Blocks for decimals:
When using base ten blocks for decimals, you would pretty much do the same thing as you would for an integer. For example, 6.84 would be shown through 6 flats, 8 longs, and 4 units.
Expanded Form:
Expanded form is the same as it is for integers when you are writing out the whole number, but it changes when you are doing the decimals. Any number after the decimal would be raised to the negative power. For example, 34.26 would be shown through 3(10)^1+4(10)^0+2(10)^-1+6(10)^-2
Decimals as fractions:
.2= 2/10
.125= 125/1000
Integers
When completing any operation with integers, if you are missing a number that you need (positive or negative), you must add a zero pair. For example, -4 - 1 requires you to take away one positive when using the chip method (or charged field). You have 4 red (negative) chips, but you cannot take away a positive from this, so you add two chips, one positive and one negative. Then, you can take away the positive and realize that you are left with -5.
Positives/Negatives:
Addition: when adding integers, two negatives equals and negative and two positives equals a positive.
Subtraction: When subtracting, if you have to subtract a negative away from the first number, you will actually add a positive. For example, 12-(-4)--->12+4. Two positives also equals a positive.
Multiplication: When multiplying, two negatives equals a positive and two positives equals a positive.
Pattern Method:
The pattern method helps you to find what your answer is by creating a pattern.
ex: (-3) x (4) = ?
3 x 4 = 12
2 x 4 = 8
1 x 4 = 4
0 x 4 = 0
-1 x 4 = -4
-2 x 4 = -8
-3 x 4 = -12
By creating a pattern with the problems you do know, you can find the answer to your problem.
Division:
-Partition: When you are partitioning a number, you will know how many items there are, how many groups there are, but will not know how many are in each group.
-Measurement: When you are using measurement, you know the amount of items and how many are in each group, but you don't know how many groups you have total.
-You can also use the pattern method for integer division.
Number Lines:
-Number lines are great tools to use when working with integers because integers include negative numbers, as well. For example, you could show the temperature starts at 20 degrees and then drops down to -4 degrees. The number line is a perfect representation of how much change has occurred between the two numbers.
Chip Method:
-The Chip Method is used to show numbers that are positive and negative. Negative numbers are used represented through a red (or colored in) chip. The positive numbers are represented through a white (or open) chip.
Absolute Value:
-The absolute value of a number is the quantity or worth of a number. It doesn't matter if the number itself is positive or negative, the absolute value is always positive. For example, the absolute value of -100 is 100. It is shown by using brackets, ex: |-100|
Whole Numbers
Number Theory
Factors:
-Factors are the numbers that a number is divisible by.
-Factor Rainbows are used as a visual aid to show which numbers are multiplied together to get the final product. The numbers that get multiplied together are the factors.
Prime and Composite Numbers:
-Prime numbers are numbers that are only divisible by one and itself and are two different factors. For example, the only factors of 7 are 1 and 7.
-Composite Numbers are numbers that have more than 2 factors. For example, the factors of 8 are: 1,2,4,and 8.
Divisibility Tests:
-Divisibility tests are used to help determine whether or not a number is a factor of another number. They are important because they save time on division of big numbers and help you to find the factors of a number.
Divisibility Test Rules:
2: Ones digit is 0,2,4,6, or 8
3: Sum of the digits is divisible by 3
4: The number formed by the last 2 digits is divisible by 4
5: One digit is 0 or 5.
6: The number is even and the sum of it's digits is divisible by 3.
8: The number formed by the last 3 digits is divisible by 8.
9: The sum of the digits is divisible by 9.
10: The ones digit is 0.
Strategies
-Regrouping: When using regrouping, students will regroup numbers into different numbers that they can easily add, subtract, multiply, or divide.
ex: 425+176
425
+ 176
------------
500
90
+ 11
-----------
500
100
+ 1
----------
601
-Subtraction Comparison: When using subtraction comparison, students will break the two numbers up into numbers that can be easily subtracted.
ex: 60-42=?
60-->40 and 21
42-->40 and 2
40-40=0, 21-2=19
-Open Number Line: When using an open number line, students can start at one of the numbers from the equation and then move or jump to whatever place they need to get to.
ex: 61-42:
-Number line will start at 61. One jump backwards (-40), gets you to 21. Another jump backwards (-2), gets you to 19.
Algorithms
-Partial Sum Algorithm: When using the partial sum algorithm, students will add the tens place first, then add the ones place. Finally, they will add the tens and ones numbers together to get their final answer.
ex: 48+33:
-40+30=70
-8+3=11
-70+11=81
-Expanded Notation: When using expanded notation, students will expand each number into different place values (thousands, hundreds, tens, ones, etc.). Next, they will add their answers together.
ex: 48+33:
-40+8
-30+3
-=80+1=81
Algorithms/Alternate Algorithms:
-Short Division: (only works for one digit divisors)
----Short Division is very similar to the traditional algorithm, but there is less work shown. For a problem like 537/4, you would:
-Determine that 4 goes into 5 one time. Put the one on the top of the equation and then figure out how much is left. 5-4 is one, so the extra one gets added onto the 3, making it worth 13.
-Determine that 4 goes into 13 three times. Add the three to the top of the equation and then figure out how much is left. 13-12 is one so the one gets added to the 7, making it worth 17.
-Determine that 4 goes into 17 four times. Put the four on the top of the equation and then determine how much is left. 17-16 is one so the one becomes your remainder.
-The final answer will show that 537/4=134 Remainder 1.
Repeated Subtraction or Partial Sum Quotient:
-This method is used by multiplying numbers by the number you are dividing by.
----For example, to show 537/4, you would:
-Show that 100x4=400 on the side of the paper. Then, subtract 400 from 537. Your number does not go on top of the equation just yet.
-Show that 10x4=40 on the side of the paper. Then, subtract 40 from 137. Your number does not go on top of the equation just yet.
-Show that 20x4=80. Subtract 80 from 97. Your number does not go on top of the equation just yet.
-Show that 4x4=16 on the side of the paper. Then, subtract 16 from 17. Your number does not go on the top of the equation just yet.
-Add all of the numbers that you multiplied by 4 together. (100+10+20+4=134) Your answer becomes 134 with a remainder of 1.
Problem Type/Model
Addition:
-Addition-set model: Combing of two sets of discrete objects (individually separate and distinct objects)
-Addition-Linear/Number Line model: Combing of two continuous quantities (ex: like-time, quantity, distance; arrows on the number line show change)
Subtraction:
-Take Away: Start with initial quantity and remove (take away) certain amount (ex: 6 fish, take away 2)
-Missing Addend: Need to determine what quantity is needed to reach the target amount (ex: 4 + ? = 10)
-Comparison: Compare sizes of two groups to determine how much larger/smaller they are (ex: David has 5 action figures, Gloria has 7 action figures... Gloria has 2 more action figures)
-Linear: Characterized on a number line, using arrows to show change.
Multiplication:
-Repeated Addition (set): Repeatedly adding quantity of objects a specified number of times.
-Repeated Addition (model): Repeatedly adding a quantity of continuous quantities (ex: 9x5)
-Area Model: Product of two numbers representing sides of a rectangle region, such that the product represents the number of unit sized squares.
Division:
-Partition (or sharing): Distributing given quantity among specified number of groups to determine the number in each group.
-Measurement (Repeated subtraction): Using given quantities to create groups of a specified size to determine the number of groups formed.
Properties
Properties for Addition:
1. Closure Property of Addition: When adding two whole numbers together, the sum will be a whole number (Addend + Addend = Sum)
2. Commutative Property of Addition: When adding, changing the order of the addends will still result in the same sum. (ex: a+b=b+a)
3. Associative Property of Addition: When adding three numbers together, changing the numbers that are grouped together will not change the sum [ex: a+(b+c)=(a+b)+c]
4. Identity Property of Addition: When adding zero to any number, the sum will be the same number (ex: a+0=a=0+a)
Properties for Subtraction:
-None of the addition properties can be used correctly for subtraction.
Properties for Multiplication:
1. Closure Property of Multiplication: When multiplying two whole numbers together, the product will be a whole number (ex: 6x7=42)
2. Commutative Property of Multiplication: When multiplying, changing the order of the factors will still result in the same sum. (ex: 6x7=7x6)
3. Associative Property of Multiplication: When multiplying three numbers together, the order of the grouping will not change the product [ex: 5x(6x7)=(5x6)x7]
4. Identity Property of Multiplication: When multiplying by one, the product will be the same number (ex: 9x1=9=1x9)
5. Zero Property of Multiplication: When multiplying anything by zero, the answer will be zero. (ex: 8x0=0, 5x0=0)
6. Distributive Property of Multiplication over addition/subtraction: (ex: addition; 3(8+15)=8x3+15x3) (ex: subtraction; 3(10-2)=3x10-3x2)
Properties of Division:
-None of the above properties apply when using division.
-There are four main operations that can be done with whole numbers.
The four operations are:
1. Addition
2. Subtraction
3. Multiplication
4. Divison
Fractions
Operations
Addition:
- When adding fractions, you must get a common denominator.
- For example: 1/2 + 2/5 = ?
- 1/2 x 5/5 = 5/10
- 2/5 x 2/2 = 4/10
- 5/10 + 4/10 = 9/10
Subtraction:
- When subtracting fractions, you must get a common denominator.
- For example: 3/4 - 1/2 = ?
- 1/2 x 2/2 = 2/4
- 3/4 - 2/4 = 1/4
Multiplication:
- When multiplying fractions, you do not need a common denominator. The top and bottom of the fraction get multiplied. Often times, it is necessary to simplify the end fraction.
- For example, 2/4 x 3/6 = ?
- 2 x 3 = 6
- 4 x 6 = 24
- Final Product = 6/24 or 1/4
Concepts
Fair Share Models:
-Area/Region Model: can have rows and columns, can be a circle, etc.
-ex: split 3 brownies between 2 people: each person gets 1 and 1/2 brownies
-Linear/Length Model: In the linear model, the model makes a line. For example, you have 3 twizzlers to split between 2 friends. Each person gets 1 1/2 twizzlers.
-Set Model: A set model has sets of objects to show fractions. For example, to show a group has 3 people with long hair and two people with short hair, you could draw 3 circles with hair and 2 circles without hair.
Equivalent fractions are when two fractions are equal in size. For example, 1/2 is equivalent to 2/4. To figure this out, you would multiply 1/2 by 2/2 (1) to get 2/4. This is called identity, when anything times 1 is equal value.
Numeration Systems
Bases
Bases change, depending on which numeration system they are attached to.
-Base 10 Digits: 0,1,2,3,4,5,6,7,8,9
-Base 2 Digits: 0,1,
-Base 5 Digits: 0,1,2,3,4
-Base 12 Digits: 0,1,2,3,4,5,6,7,8,9,x,E
Different Systems
There are many different numeration systems that vary based upon their country of origin.
-Hindu-Arabic: The Hindu-Arabic system is most commonly used in the United States. It uses the base 10 system and counting numbers 1,2,3,4,5,6,7,8, and 9.
-Tally System: The tally system uses tally marks to count. It goes up to groups of 5 and then starts a new group.
-Mayan System: The Mayan System uses base 5 and counting numbers 1,2,3,4,5,6,7,8, and 9.
-Roman Number System: This system uses Roman Numerals to count. The Roman Numerals are various different combinations of letters.