Les attitudes face aux mathématiques et l'apprentissage socioémotionel
Habiletés socioémotionnelles
Pensée critique et créative
Conscience de soi et sentiment d’identité personnelle
Relations saines
Motivation positive et persévérance
Gestion du stress et adaptation
Reconnaissance et gestion des émotions
Jo Boaler,Youcubed
ressources, vidéos, témoignages pour rendre l’enseignement et l’apprentissage des mathématiques plus visuels et engageants
développer un état d'esprit positif en salle de classe
Les processus mathématiques
“Les processus mathématiques peuvent être envisagés comme des processus par lesquels tous les élèves acquièrent et mettent en application des connaissances, des concepts et des habiletés mathématiques. Ces processus sont interreliés.” (Programme-cadre de mathématiques, 2020)
Les premiers 20 jours de mathématiques
"Des normes positives à appliquer en classe de mathématiques'
"Il y a des preuves convaincantes que le développement des habiletés socioémotionnelles à l’école contribue à la santé générale des élèves et à leur bien-être, ainsi qu’à l’amélioration de leur rendement scolaire." (Programme-cadre, 2020)
Données: le mode - médiane - moyenne
mesures de tendance centrales
L'étendue
Médiane
Mode
Moyenne
permettent de visualiser, attribuer un sens aux données
diagramme, infographie, logigramme
3 niveaux de compréhension (littératie statistique)
1) lire des données
2) lire entre les données
3) lire au-delà des données, faire des déductions
processus d'enquête
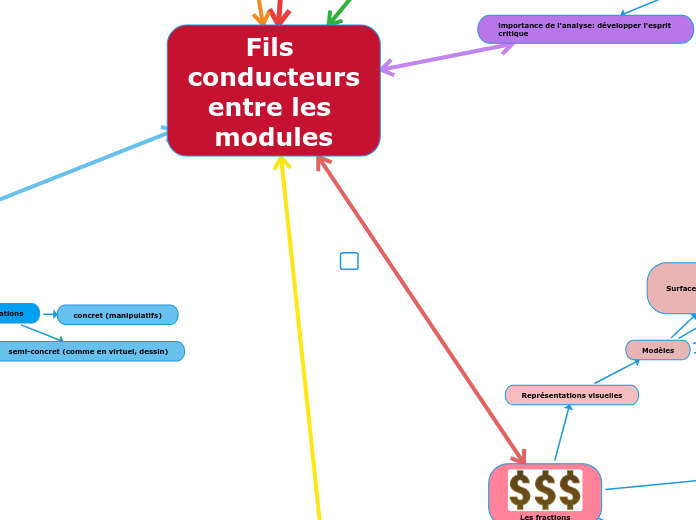
importance de l'analyse: développer l'esprit critique
GEEM traitement des données et probablité: pgs 92-100 surtout les sections de pistes de questionnement
Jouons au hockey - la probabilité
Sens de l'espace
raisonnement spatial
géométrie dynamique
interrelations!
étude unique des solides et figures planes NON!!
«quand les choses bougent, les enfants sont plus attirés, engagés et questionnent»Dr. Sinclair
liée à la réussite d'arithmétique, problèmes écrits, algèbre, géométrie
sens de la mesure
4 étapes de la mesure
3) déterminer la mesure
4) communiquer le résultat
2) choisir l'unité de mesure
1) déterminer l'attribut à mesurer
compréhension , comparaison des attributs, des concepts, des procédures et relations entre eux
malléable
manipulation d'objets
Tangram
aide à explorer le monde autour de nous
Mettre l'accent sur le raisonnement spatial
toytheater
Les fractions
jasettes fractions
parcours d'apprentissage: les fractions
Concepts clés
nombres décimaux
fractions repères
aide les élèves à pouvoir comparer/ordonner des fractions
aide les élèves à pouvoir situer d'autres fractions
fraction unitaire
numérateur toujours 1
meilleure compréhension de chaque partie de la fraction et la relation entre les deux
Fractions dans notre quotidien
Les arts
jeux
Musique
Construction, couture
Recettes
Représentations visuelles
Modèles
Ensemble
Longueur
Volume
Surface
L'algèbre - Les égalités
Les stratégies, les propriétés et les modèles en algèbre
représentations
explication orale
symbolique
semi-concret (comme en virtuel, dessin)
concret (manipulatifs)
L'inconnue et la variable
Variable
Terme indéterminé qui peut être remplacé par plusieurs valeurs
L'inconnue
Une quantité dont la valeur n’est pas encore déterminée.
Le sens de l’égalité et le sens du symbole
Sens du symbole
Relations
Opérations
Quantités
Le sens de l'égalité
Le raisonnement arithmétique (calculs) vs le raisonnement algébrique
la généralisation
Le chemin vers la généralisation
1) Observer et analyser une situation
2) Proposer une conjecture
3) Justifier une conjecture
4) Formuler une généralisation
Définition
GEEM algèbre 4e à 6e pg. 8 à 19
Activité algèbre - Atelier.on.ca
Le processus de résolution de problèmes
Différentes approches en résolution de problème
Les problèmes en 3 actes
La modélisation mathématique
1. Comprendre le problème (CONTEXTUALISÉ)
2. Analyser la situation (DÉCONTEXTUALISER)
3. Créer un modèle mathématique
4. Analyser et évaluer le modèle
**Tu ne peux pas faire la modélisation mathématique sans faire les autres processus**
Problèmes sans nombre
Je remarque, je me demande
La discussion mathématique
5) Faire des liens
4) Créer une séquence
3) Sélectionner
2) Monitorer
1) Anticiper
Permet de cibler ton questionnement, choisir l’ordre des traces d’élèves et diriger ton questionnement.
Pourquoi la créativité est si importante?
Traduction libre de « Why creativity is important? » de Bryan Mathers
Pourquoi enseigner par résolution de problème
Permettre différentes approches et styles d’apprentissages
Pratiquer la résolution de problèmes
Permettre aux élèves de comprendre la raison d’être des mathématiques
Permet la pratique de concepts et d’habiletés
Développer la confiance et maximiser le potentiel de compréhension
Développer la persévérance
Comprendre les réflexions/raisonnement de leurs élèves, comment ils peuvent utiliser leurs stratégies et outils mathématiques
Donner un sens aux maths
Un bon problème....
fait réfléchir les élèves
incite la communication et la collaboration;
permet diverses stratégies ou solutions
engage l’élève et l’incite à la persévérance
permet un point d’entrée à tous
répond à l’intention
Ressource "coup de coeur"
Make Math Moments
Les maths en 3 actes - Kyle Pearce
InfoMATHeur
Bonnes questions – L'enseignement
différencié des mathématiques
de Marian Small
la représentation
modélisation mathématique (utiiliser les situations de la vie de tous les jours pour comprendre les mthématiques)
Fils conducteursentre les modules
Le matériel de manipulation
important de cibler le concept afin de choisir le matériel approprié
À TOUS LES NIVEAUX
DIFFÉRENCIATION
un matériel pluseiurs concepts
modes de représentation
abstrait "symbolique"
semi-concret "voir" (un dessin)
concret "faire"
Ressources "coup de coeur"
Cybersavoir: quel matériel de manipulation utilisé?
Edugains - manipulative use
ACCESSIBILITÉ! pour tous
communication, raisonnement et justification
VVV (Visualiser, Verbalier et Vérifier)
Processus mathématique
le processus de résolution de problème
Représentations concrètes
papier quadrillé
Cubes emboitables
Tirer des conclusions valables,
vraies dans tous les cas, à partir de l’observation et de l’analyse de quelques exemples....Généraliser est à la base de l’acquisition des concepts et des possibilités d’abstraction (GEEM, Modélisation et Algèbre, 4e à 6e, p. 9)
inégalité
Combien serait nécessaire pour que les quantités soient pareilles ou que la situation soit juste?
RÉÉTABLIR L'ÉGALITÉ
équivalence
Nombres - comparaison
égalité
Nombres - Problèmes de réunion et ajout
L'importance de planifier des questions de consolidation - Marian Small
Les techniques d’interactions verbales favorisent et encouragent la participation des élèves