по joseph alejandro palacio soto 3 лет назад
269
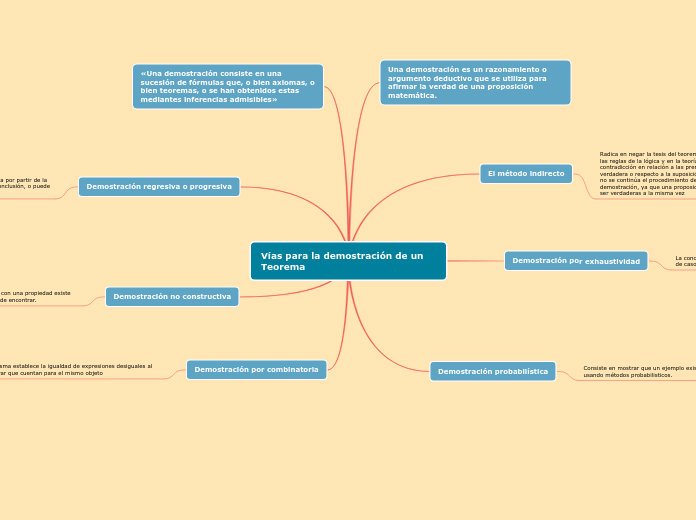
Vías para la demostración de un Teorema
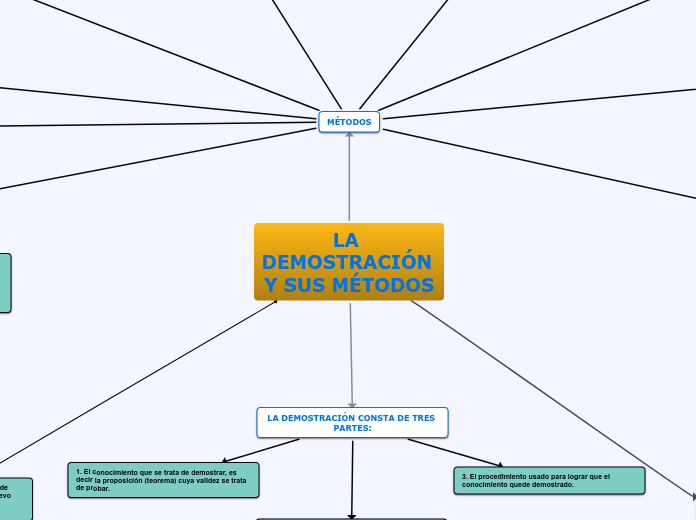
Las demostraciones matemáticas son herramientas esenciales para validar proposiciones. Existen múltiples métodos para realizarlas, cada uno con sus propias características y aplicaciones.