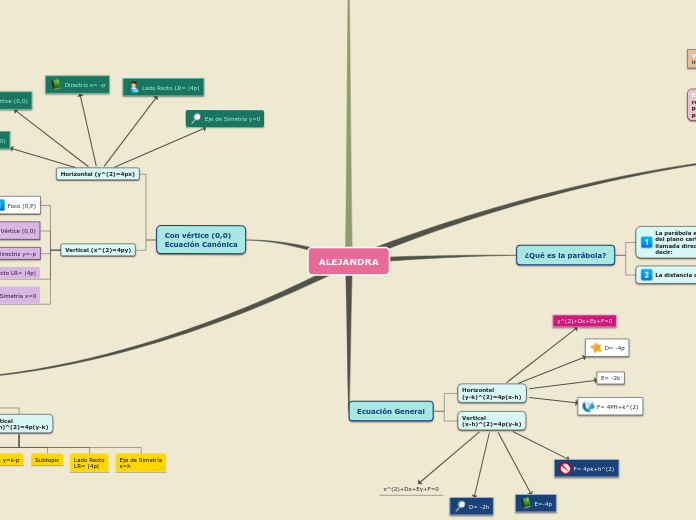
ALEJANDRA
Con vértice (h,k)
Ecuación Canónica
Eje de Simetría
x=h
Subtopic
Directriz y=k-p
Foco (h,k+p)
Eje de Simetría
y=k
Lado Recto
LR= |4p|
Directriz x=h-p
Vértice (h,k)
Foco (h+p,k)
Con vértice (0,0)
Ecuación Canónica
Vertical (x^(2)=4py)
Eje de Simetría x=0
Directriz y=-p
Foco (0,P)
Horizontal (y^(2)=4px)
Eje de Simetría y=0
Foco (P,0)
Lado Recto LR= |4p|
Directriz x= -p
Vértice (0,0)
Ecuación General
Vertical
(x-h)^(2)=4p(y-k)
x^(2)+Dx+Ey+F=0
F= 4pk+h^(2)
E=-4p
D= -2h
Horizontal
(y-k)^(2)=4p(x-h)
D= -4p
y^(2)+Dx+Ey+F=0
E= -2k
F= 4PH+k^(2)
¿Qué es la parábola?
La distancia desde (P,d)= d(P,f)
La parábola es el lugar geométrico de los punto P(x,y) del plano cartesiano que equidistan de una recta fija llamada directriz y de un punto fijo llamado foco, es decir:
ELEMENTOS
Foco.- Se representa con la letra "F" y es el punto sobre el eje de simetría que está separado del vértice, por una distancia exactamente igual a la que separa el vértice de la directriz.
Directriz.- Se representa con la letra "d", es la recta perpendicular al eje de simetría tal que la distancia del vértice a la directriz es igual a la distancia del vértice al foco.
Lado Recto.- Se representa con las letras "LR", y es la cuerda perpendicular al eje de simetría y paralela a la directriz y que pasa por el foco. (Su longitud es 4 veces la distancia del vértice al foco).
Eje de Simetría.- Conocido también como "eje focal" se representa con la letra "l" y es la recta que divide a la parábola en 2 partes iguales, (el foco y el vértice son parte de esta recta).
Vértice.- Se representa con la letra "V" y es el punto de intersección entre la parábola y el eje de simetría.
Jennifer Ocampo
3ero BGU "B"