Algebra A
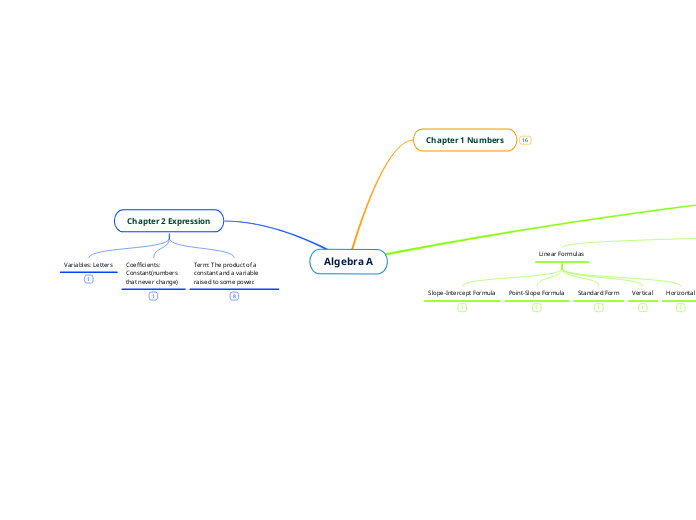
Chapter 2 Expression
Term: The product of a constant and a variable raised to some power.
Others
420x^5+69x^4+420x^3-69x^2+420x
Polynomial: Four Terms
69x^4+420x^3-69x^2+420x
Trinomial: Three Term
420x^3-69x^2+420x
Binomial: Two Terms
69x^2-420x
Coefficients: Constant(numbers that never change)
69 and 420
Variables: Letters
X, Y
Chapter 3 Equations
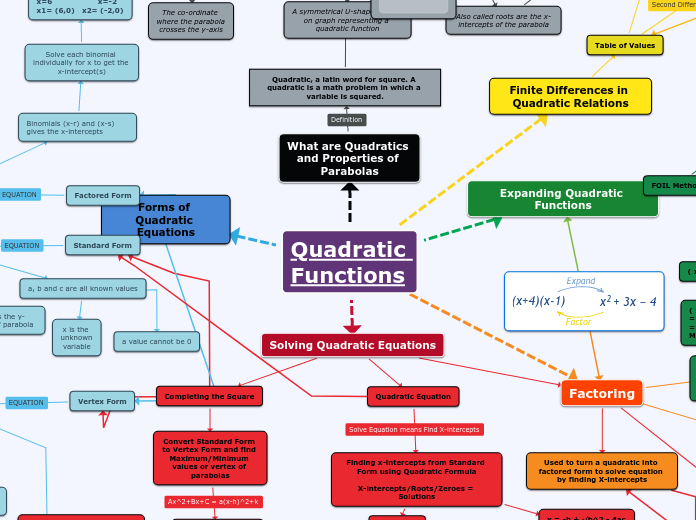
Quadratic Equation
Solving Quadratics
(-b±√(b²-4ac))/(2a)
Factoring
General Quadratics
Monic Quadratics
When we turn x^2+bx+c to (x+r)(x+s), we need to use r+s=b rs=c
Vertex: A point where two curves meet
Shapes
a<0
Facing down
a=0
Line
a>0
Facing up
Roots
Vieta's Formula
x1+x2=-b/a; x1x2=c/a
Intercept Formula: Discriminant b2-4ac
Negative
Positive
Quadratic Formula
Factored
f(x)=a(x-r)(x-s)
A(x-h)^2+K
General
Ax^2+Bx+C=0
Linear Equation
Slope
Shape
Undefined: The line is vertical
0: The line is horizontal
Negative: The line goes downward as it goes from left to right.
Positive: The line goes upward as it goes from left to right
Relationship
Perpendicular: m1m2=-1
Parallel m1=m2
Undefined
Formula
(y1-y2)/(x1-x2)
Graphing
Distance
√[(x₂ - x₁)² + (y₂ - y₁)²]
Mid-Point
[(x)1 + (x)2]/2, [(y)1 + (y)2]/2
Linear Formulas
Horizontal
y=b
Vertical
x=a
Standard Form
Ax+By=C
Point-Slope Formula
y-y1=x(x-x1)
Slope-Intercept Formula
y=mx+b
Chapter 1 Numbers
Rational Numbers: Numbers that can be written as a fraction
integers
Negative Integers -420
Whole Numbers 69
Zero
Natural Number/Positive Integer
Prime Number 7
Composite Number(number that can be divisible by more than just itself and 1) Example: 69
1
Non integers
Mixed Units 69^(69/420)
Fractions 69/420
Decimals 69.420
Irrational Numbers: Numbers that cant be written as a fraction
sqrt69
π