av juan alfredo Quispe Claros för 2 årar sedan
240
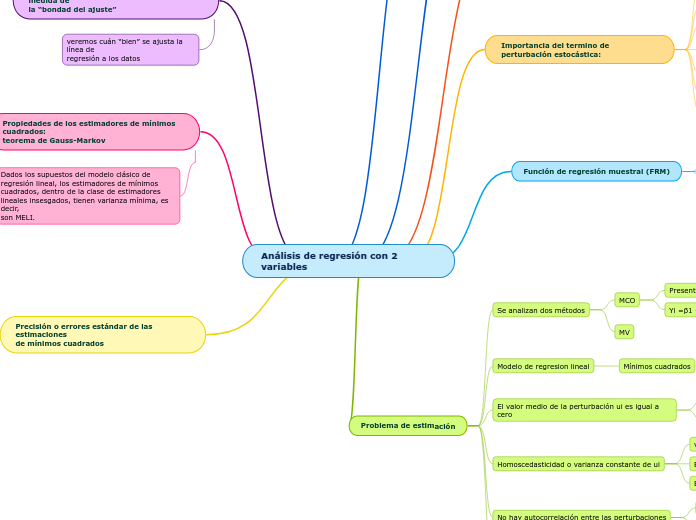
Análisis de regresión con 2 variables
En el contexto del análisis de regresión con dos variables, se destaca la importancia de la perturbación estocástica, que representa todas las variables omitidas que pueden influir en la variable dependiente.