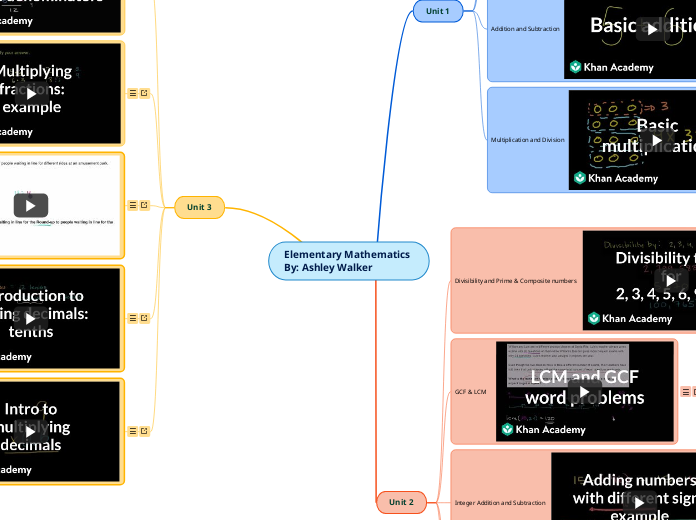
Elementary Mathematics
By: Ashley Walker
Unit 3
Multiplying and Dividing Decimals
Multiplying and Dividing Decimals:
- algorithm for multiplying decimals: if there are x digits to the right of the decimal in number 1 and y digits to the right in number 2 then the product = x+y digits to the right of the decimal
- We can also use base ten blocks to show multiplication and division
- Dividing decimals can be shown with:
- Repeated subtraction
- equal groups or partition model
- 10 by 10 grid
- Estimation can be useful when multiplying and dividing decimals.
- Example: estimate then multiply 2.3 * 3.3: we can estimate 2* 3 and then know that our answer should be more than 6. Our answer is 7.59
- More notes here: https://docs.google.com/document/d/1pgvIDQaQ2F8UxN4MjBkFlWJcADyTA8qt6hmRn0uAnvg/edit?usp=sharing
Adding and Subtracting Decimals
Adding and Subtracting Decimals:
Ratio and Proportional Reasoning
Ratio and Proportional Reasoning:
Multiplying and Dividing Fractions
Multiplying and Dividing Fractions:
Multiplying Fractions:
Dividing Fractions:
Adding and Subtracting Fractions
Adding and Subtracting Fractions:
Adding Fractions:
- Adding with like denominators: a/b + c/b = a+c/b
- Example: 2/7+ 3/7 = 5/7
- Adding with unlike denominators: we have to replace the fraction it gives us with an equivalent fraction that has like denominators
- Example: 3/5+ 1/2= 3(2)/5(2) + 1(5)/2(5) = 6/10 + 5/10= 11/10
- Ways to show the addition of fractions:
- Fraction Circle Model
- Numberline Model
- Area Model
- All shown here: https://docs.google.com/document/d/1L-zwjykVERma78gA-5ycvBaGU4zGw4mn-ZIc-uXfSMI/edit?usp=sharing
- Mixed numbers: the sum of an integer and a proper fraction
- Adding mixed numbers: additive inverse property of rational numbers= a/b + (-a/b) = 0
- Example: 2/3+ (-2/3) = 0
Subtracting Fractions:
Unit 2
Fractions
Fractions:
- Rational numbers: introduced as fractions
- Proper: Rational number that is less than 1
- Improper: Rational number greater than 1
- Numerator: how many of these parts are under consideration
- Denominator: how many equal parts has the unit been subdivided into
Numerator
------------------------
Denominator
- Comparing Fractions: ways to find if a fraction is less than or greater than another
- More same sized parts--If the numbers have the same denominator, which has the greater numerator.
- Samer number but different sized parts - If the numbers have the same numerator, which has the smaller denominator.
- More and less than one half or one whole-find which fraction is over 1 or under 1/2
- Closeness to one half or one whole -find which fraction is closer to either 1 or 1/2
Integer Multiplication and Division
Integer multiplication and division:
Integer Addition and Subtraction
Integer addition and subtraction:
- Integer: a whole number
- Negative integers= the opposite of positive ones.
- Example: -5 = the opposite of 5
- Absolute value:
- The distance between the point of an integer and 0.
- Example: absolute value of 4 = 4 shown as |4|= 4
- Integer addition models:
- Chip model: positive shown with yellow chips, Negative shown with red chips. One red neutralizes one yellow and makes a zero pair.
- Numberline model: Always start at zero, if the number is positive walk forward. If the number is negative walk backward.
- Examples of both are here: https://docs.google.com/document/d/1jQzP90452hE1c26rNnTtekByYSqiPujhf2R9F1AN3SY/edit?usp=sharing
- Properties of integer addition:
- Closure property: a+b= a unique number
- Communicative property: a+b=b+a
- Associative property: (a+b)+c= a+(b+c)
- Identity property: 0+a=a=a+0
- Integer subtraction models:
- Chip model
- Numberline model: same rules as addition, but subtraction is modeled by turning around and facing the left/ negative direction.
- Subtraction using the opposite approach: a-b=a+-b
- Examples of all here: https://docs.google.com/document/d/1jQzP90452hE1c26rNnTtekByYSqiPujhf2R9F1AN3SY/edit?usp=sharing
GCF & LCM
GCF & LCM:
- GCF= Greatest common factor.
- The greatest whole number that divides two numbers
- LCM= Least common multiple.
- The least whole number that is a multiple of both the two given numbers.
- Ways to find GCF and LCM:
- Bar model method: Build a model of 2 or more whole numbers with different colored rods.
- Slide Method: find a common factor that divides each number, divide them all then write them underneath, repeat if you have any more in common.
- Prime factorization method: Find the prime factorization of each number.
- GCF= what prime factors they have in common
- LCM= which one has the most, then multiply them.
- Examples of all here: https://docs.google.com/document/d/10JjU1xWLiRQtPZVybHgRF-TdKw1pHpbJ1mDfTHt2z8E/edit?usp=sharing
Divisibility and Prime & Composite numbers
Divisibility:
- Divisibility refers to whether or not a number can be divided.
- Example: 2 divides 12 = 2/12
- Divisibility tests:
- A number is divisible by 3 if the sum of the digits is divisible by 3.
- A number is divisible by 4 if the two-digit number in the tens and one's place is divisible by 4.
- A number is divisible by 5 if the one's digit is a 0 or a 5.
- A number is divisible by 6 if it is divisible by both 2 and 3.
- A number is divisible by 8 if the three-digit number made by the last three digits of the number is divisible by 3.
- A number is divisible by 9 if the sum of the digits is divisible by 9.
Prime and Composite Numbers:
Unit 1
Multiplication and Division
Multiplication:
6 Properties of multiplication:
- associative:(a x b)x c= a x (b x c)
- communative: a x b= b x a
- distributive: a(b+c)= (a x b) + (a x b)
- identity: a x 1 = a
- associative
- zero: a x 0 = 0
Repeated addition:
Division:
Two models of division:
- Sharing/set (partition model): answers how many in each group
Example: Noah has 18 fruit snacks and wants to share them with his 3 friends. How many will each friend get? : 18/3= 6 fruit snacks each
- Repeated subtraction: answers how many groups
Example: Noah has 18 fruit snacks, and he wants to give each person 6. How many of his friends can he share with? : 18/6= 3 friends
- Anything divided by 0 is undefined
Addition and Subtraction
Regroup and Trade!
Adding with whole numbers:
Properties of addition:
- Closure: a+b=c
- Commutative: a+b= b+a
- Associative: (a+b) +c = (b+c) +a
- Identity: a+0= a
Different models of addition:
Subtracting with whole numbers:
None of the addition properties work when it comes to subtraction
Different types of models:
Alternate methods of subtracting:
- European method: add to both sides:
example: 73
- 27
-------------------------- becomes
74
- 37
-----------------------------
Numeration and intro to number base systems
3.1 Numeration:
- Numerals are what we see when we look at numbers. It is the name for the symbol used when we see numbers such as 2 or 9.
- Face value is the value of each number.
- Different numeration systems include the Tally numeration system, Egyptian numeration system, Babylonian numeration system, Mayan numeration system, and Hindu- Arabic numeration system.
- Place Value: based on powers of 10
Ten thousand, thousands, hundreds, tens, ones.
Number base systems:
- We usually count in base 10: 0, 1,2,3,4,5,6,7,8,9,10 and so on
- In other bases it would be as shown:
- Base 4: the only numbers available are 0,1,2,3.
- Base 5: the available numbers are 0,1,2,3,4.
- Base 2: 0,1
Course overview: We went over
the syllabus and how to access the needed materials. We
also reflected on our past math experiences.